SAT MATH PRACTICE

The best way to do well on any test is to be experienced with the content. The purpose of the content given here is teach the students the concepts and battle-tested approaches they need to know to answer all types of questions in SAT math.

The goal is for every SAT question to be a simple reflex, something the students know how to handle instinctively because they have seen it so many times.

Format of the Test :

There are two math sections on the SAT.

The first section contains 20 questions to be done in 25 minutes without a calculator.

The second section contains 38 questions to be done in 55 minutes and a calculator is permitted.

Table of Contents

1. Laws of Exponents

2. Evaluating Expressions with Exponents

3.Solving Equations with Exponents

4. Simplifying Square Roots

5. Rationalizing the Denominator

6. Percent Change

7. Simple Interest and Compound Interest

8. Percent Word Problems

9. Exponential Growth and Decay

10. Doubling Time Growth Formula

11. Half Life Decay Formula

12. Functions

13. Expressions

14. Rates

15. Manipulating and Solving Equations

16. Algebraic Manipulation Problems

17. Exponents and Radicals

18. Triangles

19. Lines

20. Interpreting Linear Models

21. Complex Numbers

22. Quadratics

23. Parabola

24. Proportions

25. Equation Solving Strategies

26. Circles

27. Angles

28. Absolute Value

29. Percentage

30. Probability

31. Exponential vs Linear Growth - Concept

32. Exponential vs Linear Growth - Questions

33. Inequalities

34. Volume

35. The Language and Tools of Algebra

36. Mean Median and Mode

37. Arithmetic Mean

38. Median

39. Trigonometry

40. Solving Problems on Triangles

41. Quadratic Equations

SAT Math Video Lesson 1

SAT Math Video Lesson 2

SAT Math Video Lesson 3

SAT Math Video Lesson 4

SAT Math Video Lesson 5

Hardest SAT Math Questions

Part - 1

Part - 2

Part - 3

Part - 4

Part - 5

Part - 6

Part - 7

Part - 8

Click here to get SAT Math practice worksheets.

Sample SAT Math Questions

Question 1 :

If f(x) = x/2 - 1, what is f(-2x + 1) equal to?

A) -x - 1/2

B) -x + 1/2

C) x - 1/2

D) x + 1/2

Answer :

f(x) = x/2 - 1

Replace x by -2x + 1.

f(-2x + 1) = (-2x + 1)/2 - 1

= -2x/2 + 1/2 - 1

= -x - 1/2

The correct answer choice is (D).

Question 2 :

If x = 1 - a/b, which of the following is equivalent to 1/x?

A) b/(1 + a)

B) b/(1 - a)

C) (b - 1)/a

D) b/(b - a)

Answer :

x = 1 - a/b

x = b/b - a/b

x = (b - a)/b

Take reciprocal on both sides.

1/x = b/(b - a)

The correct answer choice is (A).

Question 3 :

(16 - 4x)/2 = nx + 8 + 3x

If the linear equation above is an identity, what is the value of n?

A) -5

B) -3

C) -1

D) 3

Answer :

(16 - 4x)/2 = nx + 8 + 3x

16/2 - 4x/2 = 8 + nx + 3x

8 - 2x =  8 + (n + 3)x

Since the equation is identity, each side is the same.

Equate the coefficients of x.

-2 = n + 3

Subtract 3 from both sides.

-5 = n

The correct answer choice is (A).

Question 4 :

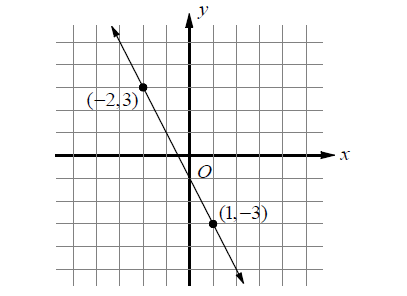
Which of the following equations represents a line that contains the point (1/2, 3) and it is parallel to the line shown above?

A) y = x + 5/2

B) y = -x + 7/2

C) y = -2x + 4

D) y = -2x + 6

Answer :

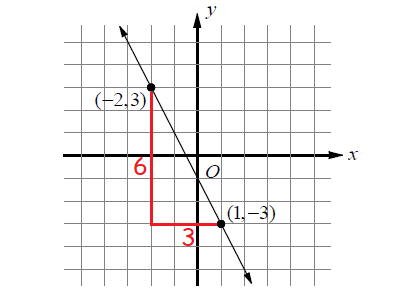
For the above line,

rise = 6

run = 3

Since the line is a falling line, the slope has to be negative.

slope = rise/run

= -6/3

= -2

Equation of the line which is parallel to the above line is 

y = -2x + b ----(1)

(since the lines are parallel, the slopes must be equal)

Since (1) contains the point (1/2, 3), substitute x = 1/2 and y = 3.

3 = -2(1/2) + b

3 = -1 + b

4 = b

Therefore, equation of the required line is

(1)----> y = -2x + 4

The correct answer choice is (C).

Question 5 :

If 2√p + 3√q = 7√q, where p > 0 and q > 0, what is p in terms of q?

Answer :

2√p + 3√q = 7√q

Subtract 3√q from both sides.

2√p = 4√q

Divide both sides by 2.

√p = 2√q

Squaring both sides.

(√p)² = (2√q)²

p = 2²(√q)²

p = 4y

Question 6 :

6x + my = 3

2x + y = n

For what values of m and n of will the system of equations above have infinitely many solutions?

Answer :

Write the given two linear equations in slope-intercept form :

6x + my = 3 :

6x + my = 3

my = -6x + 3

y = (-6/m)x + 3/m

2x + y = n :

2x + y = n

y = -2x + n

If a system of linear equations has infinitely many solutions, the two equations must be equivalent.

That is, both the equations must have the same slope and same y-intercept.

Equate the slopes.

-6/m = -2

6/m = 2

m/6 = 1/2

m = 3

Equate the y-intercepts.

3/m = n

Substitute m = 3.

3/3 = n

1 = n

Therefore, m = 3 and n = 1.

Question 7 :

William is playing a board game in which he has to collect as many cards as possible. On his first turn, he loses 18 percent of his cards. On the second turn, he increases his card count by 36 percent. If his final card count after these two turns is n, which of the following represents his starting card count in terms of n?

A) n/[(1.18)(0.64)]

B) (1.18)(0.64)n

C) n/[(1.36)(0.82)]

D) (0.82)(1.36)n

Answer :

Let x be the starting card count.

Number of cards after losing 18% of cards on the first turn :

= (100 - 18)% ⋅ x

= 82% ⋅ x

= 0.82x

Number of cards after increasing 36% of cards on the second turn :

= (100 + 36)% ⋅ 0.82x

= 136% ⋅ 0.82x

= 1.36 ⋅ 0.82x

= (1.36)(0.82)x

Given : Final card count after these two turns is n.

Then, we have

(1.36)(0.82)x = n

Divide each side by (1.36)(0.82).

x = n/[(1.36)(0.82)]

So, the starting card count in terms of n is

n/[(1.36)(0.82)]

Therefore, option C is correct.

Question 8 :

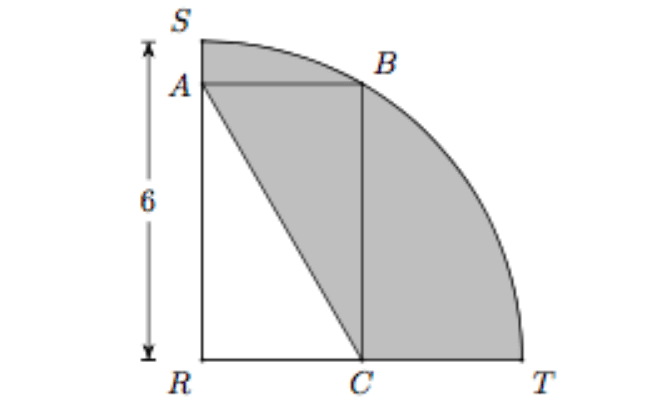
In the figure above, arc SBT is one quarter of a circle with center R and radius 6. If the length plus the width of rectangle ABCR is 8, Then the perimeter of the shaded region is

(A)  8 + π    (B)  10 + 3π

(C) 14 + 3π    (D)  8 + π

Answer :

Idea to solve this problem : 

Find the perimeter of one quarter of the circle STR. Subtract the length (AR) and width (RC) of the rectangle ABCR from the above perimeter. Then, add the  the length of the diagonal (AC).  

Step 1 :

Perimeter of one quarter of the circle STR is

=  2πr/4 + 2r

=  πr/2 + 2r

Substitute 6 for r. 

=  6π/2 + 2(6)

=  3π + 12

Step 2 :

Given : The length plus width of rectangle ABCR is 8.

Then, 

AR + RC  =  8

Subtract 8 from the perimeter found in step 1. 

=  3π + 12 - 8

=  3π + 4

Step 3 : 

The two diagonals of the rectangle ABCR are AC and RB in which RB is being as radius of the circle. 

So, RB = 6.

In any rectangle, the lengths of two diagonals are always congruent. 

Then, AC = 6. 

Add the length of the diagonal AC (= 6) to the result of step 2.

=  3π + 4 + 6

=  3π + 10

Perimeter of the shaded region is (10 + 3π).

The correct answer choice is (B).

Question 9 :

In the figure above AC is perpendicular to BC. What is the measure of m∠ABC?

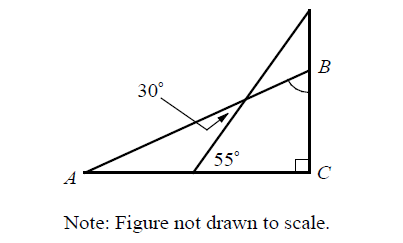
Answer :

By Exterior Angle Theorem,

m∠A + 30° = 55°

m∠A = 25°

In triangle ABC,

m∠BAC + m∠ACB + m∠ABC = 180

25° + 90° + m∠ABC = 180°

115° + m∠ABC = 180°

Subtract 115° from both sides.

m∠ABC = 65°

Question 10 :

n, n - 3, 2n - 1, 3n - 4 and 5n + 12

The average (arithmetic mean) of five numbers given above is 8. Which of of the following is true?

A) median = 5, mode = 7

B) median = 5, mode = 5

C) median = 7, mode = 7

D) median = 7, mode = 5

Answer :

Average of five numbers = 8

(n + n - 3 + 2n - 1 + 3n - 4 + 5n + 12)/5 = 8

(12n + 4)/5 = 8

Multiply both sides by 5.

12n + 4 = 40

Subtract 4 from both sides.

12n = 36

Divide both sides by 12.

n = 3

Then,

n - 3 = 0

2n - 1 = 5

3n - 4 = 5

5n + 12 = 27

The given five numbers are 3, 0, 5, 5 and 27.

Arrange the numbers from least to greatest.

0, 3, 5, 5, 27

median = 5

mode = 5

The correct answer choice is (B).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.