SAT MATH QUESTIONS ON CIRCLES

Question 1 :

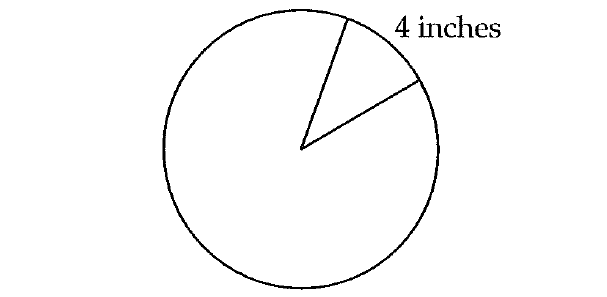
A certain pizza restaurant cuts slices out at every 4 inches along the edge of a pizza, as shown in the figure above. What is the maximum number of full pizza slices that can be cut out from a circular pizza with a radius of 10 inches?

A) 7

B) 8

C) 14

D) 15

Answer :

Circumference of the pizza :

= 2πr

= 2π(10)

= 20π

We know that the circumference of a circle is length around the circle.

To find the maximum number of full pizza slices with 4 inches along the edge of a pizza that can be cut out from a circular pizza, we have to divide the circumference 20π by 4.

= 20π/4

≈ 15.7

Since, the slices must be full slices, the answer is 15.

The correct answer choice is (D).

Question 2 :

A circle in the xy-plane is centered at (1, 2) and contains the point (4, 6). Which of the following could be the equation of the circle?

A) (x - 1)² + (y - 2)² = 5

B) (x - 1)² + (y - 2)² = 25

C) (x + 1)² + (y + 2)² = 5

D) (x + 1)² + (y + 2)² = 25

Answer :

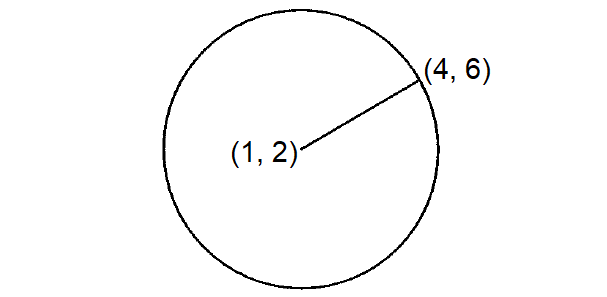
The radius of the circle above is the distance between the center (1, 2) and the point (4, 6) on the circle.

Distance between two points :

Substitute (x₁, y₁) = (1, 2) and (x₂, y₂) = (4, 6).

The radius of the circle is 5 units.

Equation of a circle in standard form :

(x - h)² + (y - k)² = r²

Here, center = (h, k), radius = r.

Substitute (h, k) = (1, 2) and r = 5.

(x - 1)² + (y - 2)² = 5²

(x - 1)² + (y - 2)² = 25

The correct answer choice is (B).

Question 3 :

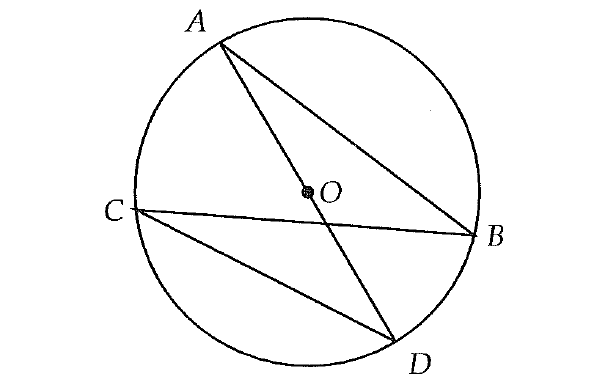
The circle above has center O. Which of the following line segments from the figure above is greatest in length?

A) AB

B) AD

C) BC

D) It cannot be determined from the information given.

Answer :

The line segment which  passes through the center of the circle is called diameter and also that is the longest segment.

In the circle above, AD is the line segment which passes through the center. So, AD is the diameter and also that is line segment greatest in length.

The correct answer choice is (B).

Question 4 :

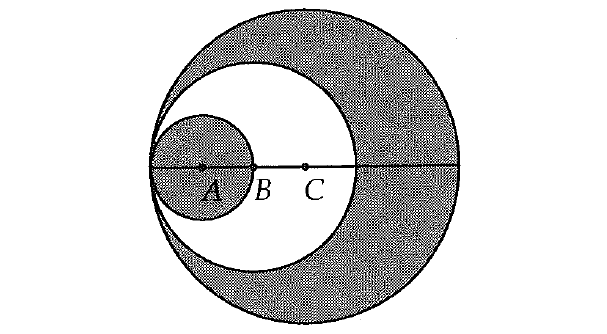
In the figure above, circle A has a radius of 2, circle B has a radius of 4, and circle C has a radius of 6. What is the area of the shaded region?

A) 18π

B) 20π

C) 22π

D) 24π

Answer :

To find the area of the shaded region, we have to subtract the area of circle B from the area of circle C and include the area of circle A.

Area of shaded region :

= Area of circle C - Area of circle B + Area of circle A

= π(6)² + π(4)² + π(2)²

= π(36) + π(16) + π(4)

= 36π + 16π + 4π

= 24π

The correct answer choice is (D).

Question 5 :

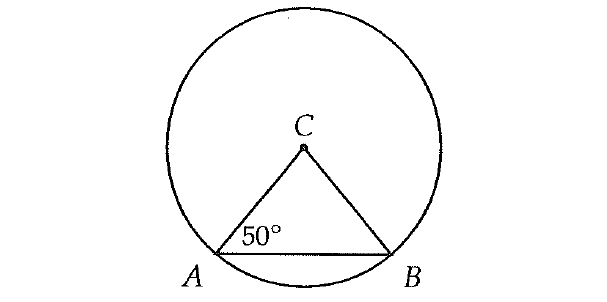
In the figure above, A and B are points on the circle C. If the area of the circle is 54π, what is the area of the sector formed by central angle ACB?

A) 10π

B) 12π

C) 14π

D) 16π

Answer :

In the figure above, ΔABC is an isosceles triangle, because AC = AB (radii are equal).

So,

∠CAB = ∠CBA = 50°

In ΔABC,

∠ACB + ∠CAB + ∠CBA = 180°

∠ACB + 50° + 50° = 180°

∠ACB + 100° = 180°

∠ACB = 80°

Formula for area of a sector :

= (θ/360°) x area of the circle

Here, θ is the central angle of the sector.

Area of the sector formed by central angle ACB :

= (80°/360°) x 54π

= (2/9) x 54π

= 12π

The correct answer choice is (B).

Question 6 :

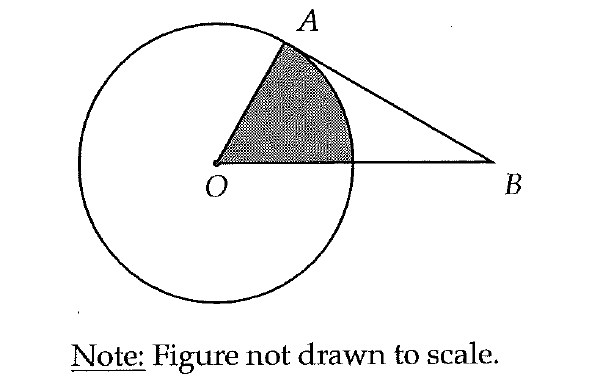
In the figure above, the circle has center O and segment AB is tangent to the circle. If angle ABO measures π/10 radians and the area of the shaded  sector is π, what is the area of the circle?

A) 5π

B) 6π

C) 8π

D) 9π

Answer :

Convert π/10 radians to degrees :

π/10 radians = (π/10) x (180°/π)

= 18°

∠ABO = 18°

Because segment AB is tangent to the circle,

∠OAB = 90°

(Angle between the tangent and radius of the circle at the point of tangency is always 90°)

In ΔABC,

∠AOB + ∠ABO + ∠OAB = 180°

∠AOB + 18° + 90° = 180°

∠AOB + 108° = 180°

∠AOB = 72°

Area of the shaded sector = π

(72°/360°) x Area of the circle = π

(1/5) x Area of the circle = π

Area of the circle = 5π

The correct answer choice is (A).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.