ORDER OF ROTATIONAL SYMMETRY

Example 1 :

What is the order of rotational symmetry of an equilateral triangle?

Solution :

As explained in the definition, we have to check how many times an equilateral triangle fits on to itself during a full rotation of 360 degrees.

Please look at the images of the equilateral triangle in the order A,B and C. A is the original image. The images B and C are generated by rotating the original image A.

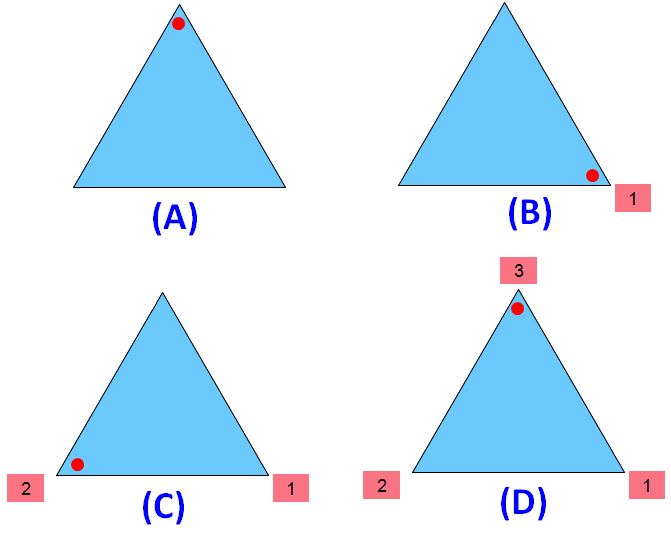
When we look at the above images of equilateral triangle, it fits on to itself 3 times during a full rotation of 360 degrees.

So, an equilateral triangle has rotational symmetry of order 3.

Example 2 :

What is the order of rotational-symmetry of a square?

Solution :

Please look at the images of the square in the order A, B, C, D and E. A is the original image. The images B, C, D and E are generated by rotating the original image A.

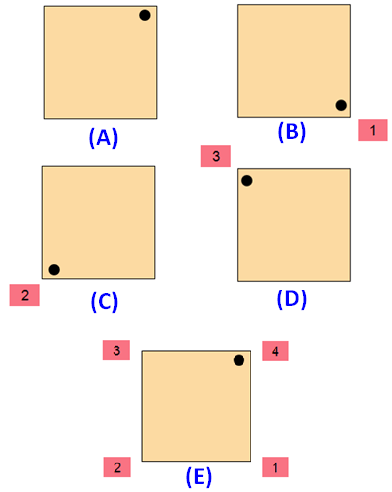
When we look at the above images of square, it fits on to itself 4 times during a full rotation of 360 degrees.

So, a square has rotational symmetry of order 4.

Example 3 :

What is the order of rotational symmetry of a regular pentagon?

Solution :

Please look at the images of the regular pentagon in the order A, B, C, D, E and F. A is the original image. The images B, C, D, E and F are generated by rotating the original image A.

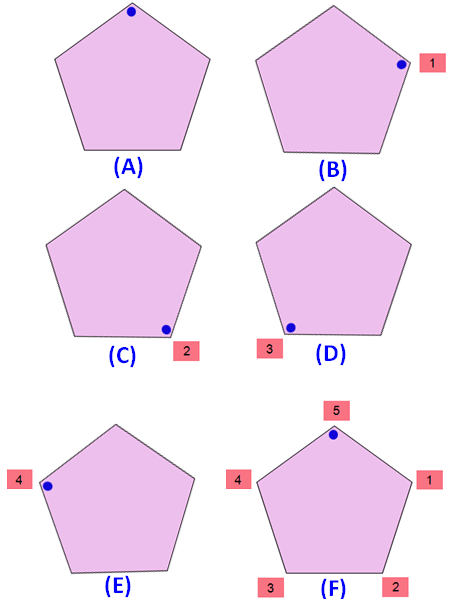
When we look at the above images of regular pentagon, it fits on to itself 5 times during a full rotation of 360 degrees.

So, a regular pentagon has rotational symmetry of order 5.

Example 4 :

What is the order of rotational-symmetry of a parallelogram?

Solution :

Please look at the images of the parallelogram in the order A, B and  C. A is the original image. The images B and C are generated by rotating the original image A.

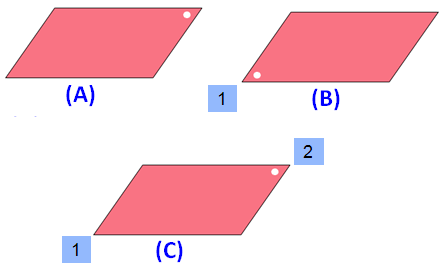
When we look at the above images of parallelogram, it fits on to itself 2 times during a full rotation of 360 degrees.

So, a parallelogram has rotational symmetry of order 2.

Example 5 :

What is the order of rotational symmetry of an isosceles triangle?

Solution :

Please look at the images of the isosceles triangle in the order A and B. A is the original image. The image B is generated by rotating the original image A.

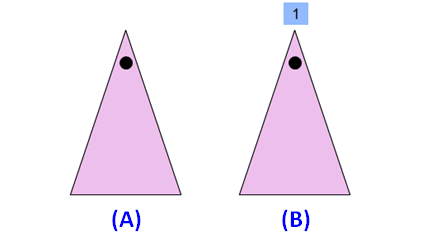
When we look at the above images of isosceles triangle, it fits on to itself 1 time during a full rotation of 360 degrees.

So, an isosceles triangle has rotational symmetry of order 1.

Example 6 :

What is the order of rotational-symmetry of a scalene triangle?

Solution :

Please look at the images of the scalene triangle in the order A and B. A is the original image. The image B is generated by rotating the original image A.

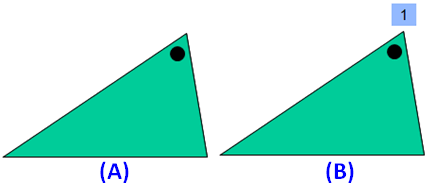
When we look at the above images of isosceles triangle, it fits on to itself 1 time during a full rotation of 360 degrees.

So, a scalene triangle has rotational symmetry of order 1.

Example 7 :

What is the order of rotational symmetry of a trapezium?

Solution :

Please look at the images of the trapezium in the order A and B. A is the original image. The image B is generated by rotating the original image A.

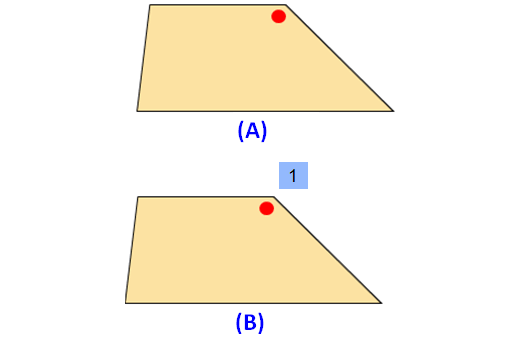
When we look at the above images of trapezium, it fits on to itself 1 time during a full rotation of 360 degrees.

So, a trapezium has rotational symmetry of order 1.

Example 8 :

What is the order of rotational-symmetry of an isosceles trapezium?

Solution :

Please look at the images of the isosceles trapezium in the order A and B. A is the original image. The image B is generated by rotating the original image A.

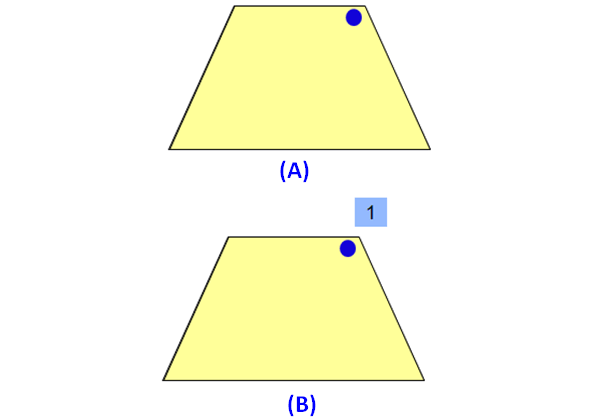
When we look at the above images of isosceles trapezium, it fits on to itself 1 time during a full rotation of 360 degrees.

So, an isosceles  trapezium has rotational symmetry of order 1.

Example 9 :

What is the order of rotational-symmetry of a kite?

Solution :

Please look at the images of the kite in the order A and B. A is the original image. The image B is generated by rotating the original image A.

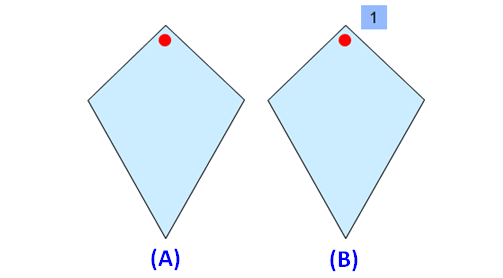
When we look at the above images of kite, it fits on to itself 1 time during a full rotation of 360 degrees.

So, a kite has rotational symmetry of order 1.

Example 10 :

What is the order of rotational-symmetry of a rhombus?

Solution :

Please look at the images of the rhombus in the order A, B and C. A is the original image. The images B and C are generated by rotating the original image A.

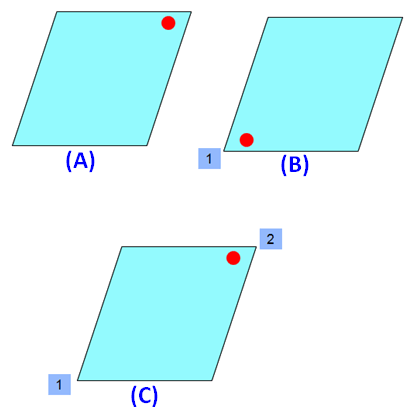
When we look at the above images of rhombus, it fits on to itself 2 time during a full rotation of 360 degrees.

So, a rhombus has rotational symmetry of order 2.

Example 11 :

What is the order of rotational-symmetry of an ellipse?

Solution :

Please look at the images of the ellipse in the order A, B and C. A is the original image. The images B and C are generated by rotating the original image A.

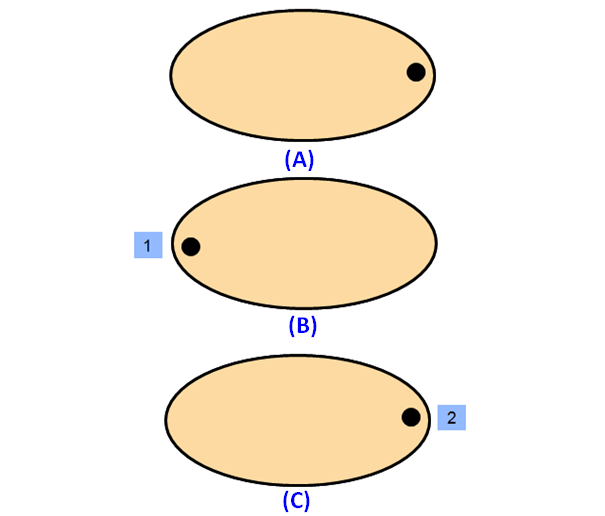
When we look at the above images of ellipse, it fits on to itself 2 time during a full rotation of 360 degrees.

So, an ellipse has rotational symmetry of order 2.

Example 12 :

What is the order of rotational-symmetry of a circle?

Solution :

A circle has an infinite 'order of rotational symmetry'. In simplistic terms, a circle will always fit into its original outline, regardless of how many times it is rotated.

So, a circle has infinite order of rotational symmetry.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.