GEMDAS ORDER OF OPERATIONS

GEMDAS is the rule that can be used to simplify or evaluate complicated numerical expressions with more than one binary operation.

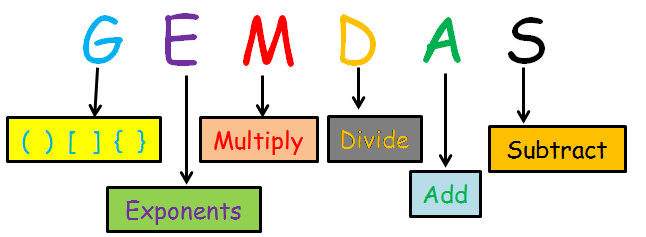
Very simply way to remember  GEMDAS rule :

G ---> Grouping (Parentheses)

E ----> Exponent

M ----> Multiply

D ----> Divide

A ----> Add

S ----> Subtract

Important Notes :

1. In a particular simplification, if you have both multiplication and division, do the operations one by one in the order from left to right.

2. Division does not always come before multiplication. We have to do one by one in the order from left to right.

3. In a particular simplification, if you have both addition and subtraction, do the operations one by one in the order from left to right.

Examples :

12 ÷ 3 x 5 = 4 x 5 = 20

13 - 5 + 9 = 8 + 9 = 17

In the above simplification, we have both division and multiplication. From left to right, we have division first and multiplication next. So we do division first and multiplication next.

Practice Problems

Problem 1 :

Evaluate :

5 + 6 x 7

Solution :

Problem 2 :

Evaluate :

(25 + 11) x 2

Solution :

Problem 3 :

Evaluate :

10² - 16 ÷ 8

Solution :

Problem 4 :

Evaluate :

3 + 6 x (5 + 4) ÷ 3 -7

Solution :

Problem 5 :

Evaluate :

56 - 2(20 + 12 ÷ 4 x 3 - 2 x 2) + 10

Solution :

Problem 6 :

Evaluate :

6 + [(16 - 4) ÷ (2² + 2)] - 2

Solution :

Problem 7 :

Evaluate :

(96 ÷ 12) + 14 x (12 + 8) ÷ 2

Solution :

Problem 8 :

Evaluate :

(93 + 15) ÷ (3 x 4) - 24 + 8

Solution :

Problem 9 :

Evaluate :

55 ÷ 11 + (18 - 6) x 9

Solution :

Problem 10 :

Evaluate :

(7 + 18) x 3 ÷ (2 + 13) - 28

Solution :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.