BODMAS RULE
The rule or order that we use to simplify numerical expressions in math is
called BODMAS rule.
Very simply way to remember BODMAS rule!
B ----> Brackets
O ----> Of (orders :Powers and radicals)
D ----> Division
M ----> Multiplication
A ----> Addition
S ----> Subtraction
Important Notes :
1. In a particular simplification, if you have both multiplication and division, do the operations one by one in the order from left to right.
2. Division does not always come before multiplication. We have to do one by one in the order from left to right.
3. In a particular simplification, if you have both addition and subtraction, do the operations one by one in the order from left to right.
Examples :
12 ÷ 3 x 5 = 4 x 5 = 20
13 - 5 + 9 = 8 + 9 = 17
In the above simplification, we have both division and multiplication. From left to right, we have division first and multiplication next. So we do division first and multiplication next.
Note :
Inside the brackets, if there are two or more operations, follow BODMAS Rule inside the brackets.
Problem
1 :
Evaluate :
5 + 3 x 12
Solution :
= 5 + 3 x 12 ----> Multiplication
= 5 + 36 ----> Addition
= 41 ----> Answer
Problem 2 :
Evaluate :
24 ÷ 6 + 72
Solution :
= 24 ÷ 6 + 72 ----> Exponent
= 24 ÷ 6 + 49 ----> Division
= 4 + 49 ----> Addition
= 53 ----> Answer
Problem 3 :
Evaluate :
3 x (27 - 16)
Solution :
= 3 x (27 - 16) ----> Brackets
= 3 x 11 ----> Multiplication
= 33 ----> Answer
Problem 4 :
Evaluate :
25 - 4 x (7 + 5) ÷ 4 + 3
Solution :
= 25 - 4 x (7 + 5) ÷ 4 + 3 ----> Brackets
= 25 - 4 x 12 ÷ 4 + 3 ----> Multiplication
= 25 - 48 ÷ 4 + 3 ----> Division
= 25 - 12 + 3 ----> Subtraction
= 13 + 3 ----> Addition
= 16 ----> Answer
Problem 5 :
Evaluate :
64 - 3(13 + 2 x 12 ÷ 8 - 3 x 3) + 11
Solution :
= 64 - 3(13 + 2 x 12 ÷ 8 - 3 x 3) + 11 ----> Brackets
= 64 - 3(13 + 2 x 12 ÷ 8 - 3 x 3) + 11 ----> Multiplication
= 64 - 3(13 + 24 ÷ 8 - 3 x 3) + 11 ----> Division
= 64 - 3(13 + 3 - 3 x 3) + 11 ----> Multiplication
= 64 - 3(13 + 3 - 9) + 11 ----> Addition
= 64 - 3(16 - 9) + 11 ----> Brackets
= 64 - 3(7) + 11 ----> Multiplication
= 64 - 21 + 10 ----> Subtraction
= 43 + 10 ----> Addition
= 53 ----> Answer
Problem 6 :
Evaluate :
[(45 - 3) ÷ (32 + 5)] x 2 - 5
Solution :
= [(45 - 3) ÷ (32 + 5)] x 2 - 5 ----> Square Brackets
= [(45 - 3) ÷ (32 + 5)] x 2 - 5 ----> Brackets
= [42 ÷ (32 + 5)] x 2 - 5 ----> Brackets
= [42 ÷ (32 + 5)] x 2 - 5 ----> Exponent
= [42 ÷ (9 + 5)] x 2 - 5 ----> Brackets
= [42 ÷ 14] x 2 - 5 ----> Square Brackets
= 3 x 2 - 5 ----> Multiplication
= 6 - 5 ----> Subtraction
= 1 ----> Answer
Problem 7 :
Evaluate :
(2 x 33 ÷ 9) - 2 x (6 + 8) ÷ 7
Solution :
= (2 x 33 ÷ 9) - 2 x (6 + 8) ÷ 7 ----> Brackets
= (2 x 33 ÷ 9) - 2 x (6 + 8) ÷ 7 ----> Exponent
= (2 x 27 ÷ 9) - 2 x (6 + 8) ÷ 7 ----> Multiplication
= (54 ÷ 9) - 2 x (6 + 8) ÷ 7 ----> Brackets
= 6 - 2 x (6 + 8) ÷ 7 ----> Brackets
= 6 - 2 x 14 ÷ 7 ----> Multiplication
= 6 - 28 ÷ 7 ----> Multiplication
= 6 - 4 ----> Multiplication
= 2 ----> Answer
Problem 8 :
Evaluate :
(120 - 12) ÷ (36 ÷ 3) - 22 + 7
Solution :
= (120 - 12) ÷ (36 ÷ 3) - 22 + 7 ----> Brackets
= 108 ÷ (36 ÷ 3) - 22 + 7 ----> Brackets
= 108 ÷ 12 - 22 + 7 ----> Division
= 9 - 22 + 7 ----> Subtraction
= -13 + 7 ----> Subtraction
= -6 ----> Answer
Problem 9 :
Evaluate :
5 x 12 ÷ 10 - (6 x 4) ÷ 12
Solution :
= 5 x 12 ÷ 10 - (6 x 4) ÷ 12 ----> Brackets
= 5 x 12 ÷ 10 - 24 ÷ 12 ----> Multiplication
= 60 ÷ 10 - 24 ÷ 12 ----> Division
= 6 - 24 ÷ 12 ----> Division
= 6 - 2 ----> Subtraction
= 4 ----> Answer
Problem 10 :
Evaluate :
(29 - 13) x 3 ÷ (15 - 7) + 8
Solution :
= (29 - 13) x 3 ÷ (15 - 7) + 8 ----> Brackets
= 16 x 3 ÷ (15 - 7) + 8 ----> Brackets
= 16 x 3 ÷ 8 + 8 ----> Multiplication
= 48 ÷ 8 + 8 ----> Division
= 6 + 8 ----> Addition
= 14 ----> Answer
Problem 11 :
Evaluate :
[96 ÷ (62 - 12) ÷ 4 - 3] x 2 + 13
Solution :
= [96 ÷ (62 - 12) ÷ 4 - 3] x 2 + 13 ----> Square Brackets
= [96 ÷ (62 - 12) ÷ 4 - 3] x 2 + 13 ----> Brackets
= [96 ÷ (62 - 12) ÷ 4 - 3] x 2 + 13 ----> Exponent
= [96 ÷ (36 - 12) ÷ 4 - 3] x 2 + 13 ----> Brackets
= [96 ÷ 24 ÷ 4 - 3] x 2 + 13 ----> Division
= [4 ÷ 4 - 3] x 2 + 13 ----> Division
= [1 - 3] x 2 + 13 ----> Square Brackets
= -2 x 2 + 13 ----> Multiplication
= -4 + 13 ----> Subtraction
= 9 ----> Answer
Problem 12 :
Evaluate :
(a2 + bc) + c3 ÷ (a2 + b) - c
if a = 3, b = -5 and c = 4.
Solution :
(a2 + bc) + c3 ÷ (a2 + b) - c
Substitute a = 3, b = -5 and c = 4.
[32 + (-5)4] + 43 ÷ [32 + (-5)] - 4
Evaluation :
= [32 + (-5)4] + 43 ÷ [32 + (-5)] - 4 ----> Square Brackets
= [32 + (-5)4] + 43 ÷ [32 + (-5)] - 4 ----> Exponent
= [9 + (-5)4] + 43 ÷ [32 + (-5)] - 4 ----> Multiplication
= [9 - 20] + 43 ÷ [32 + (-5)] - 4 ----> Square Brackets
= -11 + 43 ÷ [32 + (-5)] - 4 ----> Square Brackets
= -11 + 43 ÷ [32 + (-5)] - 4 ----> Exponent
= -11 + 43 ÷ [9 + (-5)] - 4 ----> Multiplication
= -11 + 43 ÷ [9 - 5] - 4 ----> Square Brackets
= -11 + 43 ÷ 4 - 4 ----> Exponent
= -11 + 64 ÷ 4 - 4 ----> Division
= -11 + 16 - 4 ----> Subtraction
= 5 - 4 ----> Subtraction
= 1 ----> Answer
Problem 13 :
Evaluate :
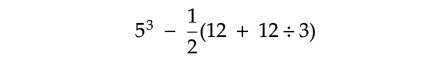
Solution :
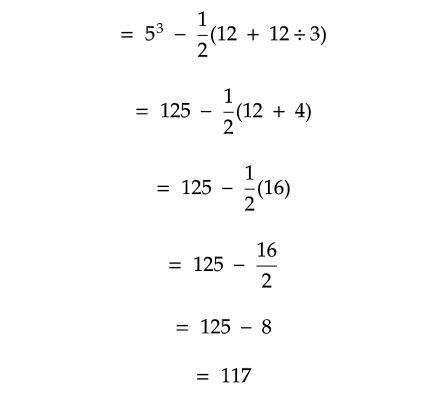
Problem 14 :
Evaluate :
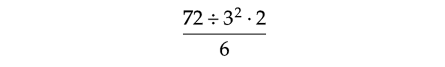
Solution :
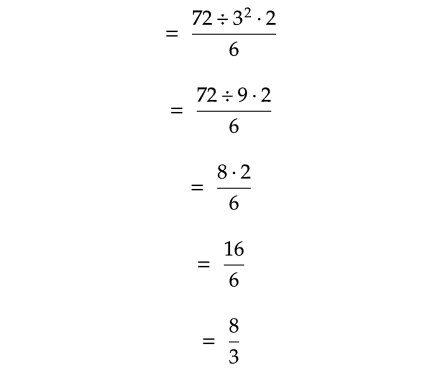
Problem 15 :
Evaluate :
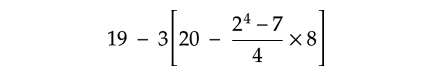
Solution :
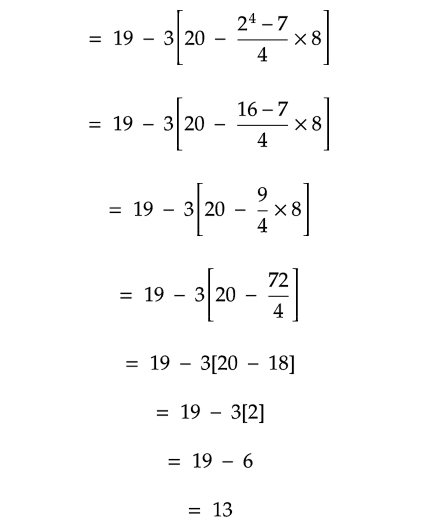
Problem 16 :
What is the value of
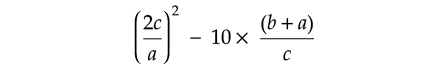
if a = -2, b = 3 and c = 5.
Solution :
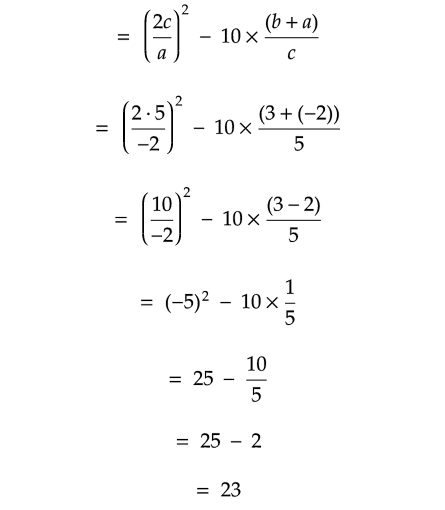
Problem 17 :
What is the value of
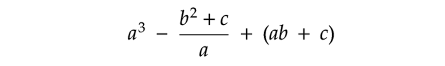
if a = 4, b = -3 and c = 7.
Solution :
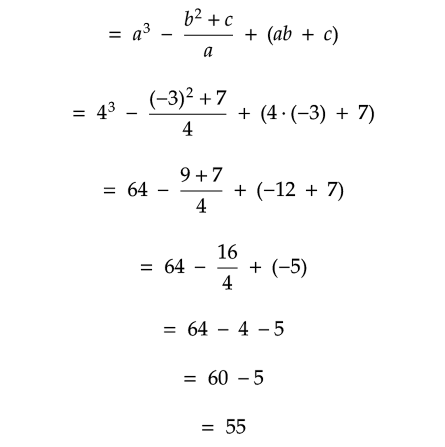
Problem 18 :
What is the value of
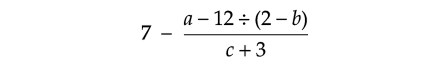
if a = 3, b = -1 and c = -2.
Solution :
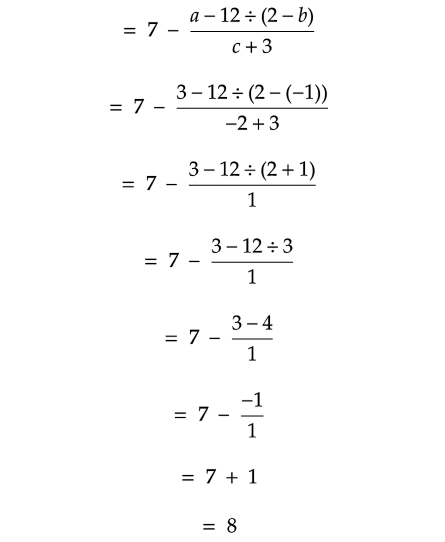
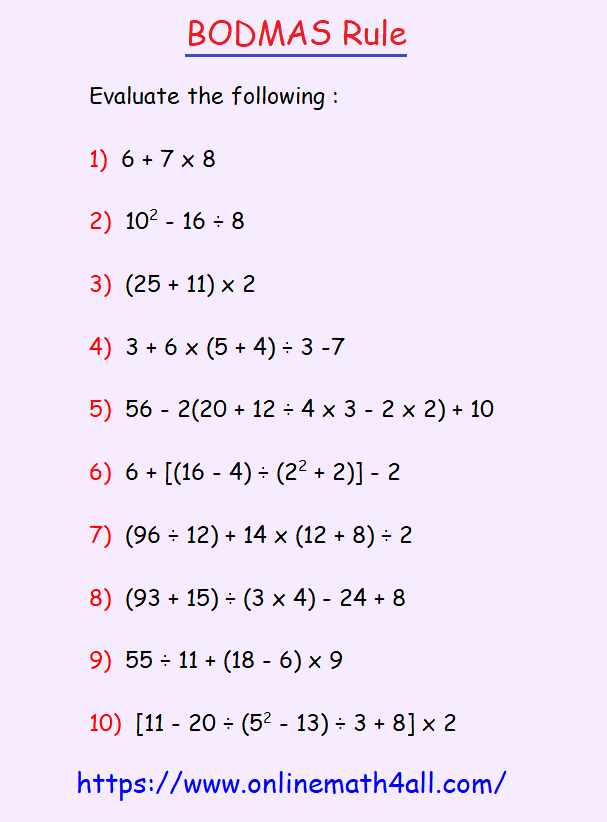
Click here to get step by step answers for the above questions.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Trigonometry Reciprocal Identities
Apr 28, 24 10:10 AM
Trigonometry Reciprocal Identities -
IB Diploma Mathematics Problems on Exponents
Apr 28, 24 05:42 AM
IB Diploma Mathematics - Problems on Exponents -
Finding Vertex of a Quadratic Function Worksheet
Apr 27, 24 11:06 AM
Finding Vertex of a Quadratic Function Worksheet
