SOHCAHTOA

This is a way to remember how values the trigonometric ratios sin, cosine and tangent of an angle can be computed.

Let us see, how this shortcut works to remember the above mentioned trigonometric ratios.

Before we discuss this shortcut, let us know the name of each side of a right triangle from the figure given below.

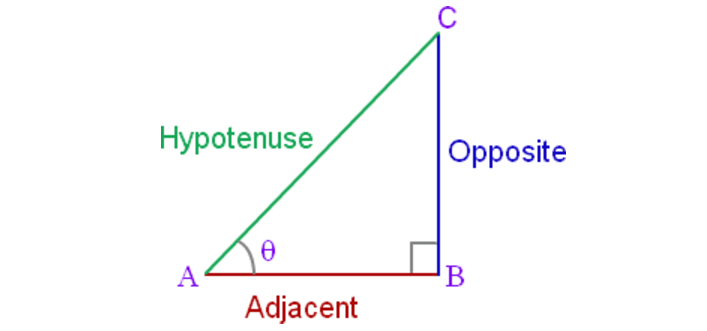
To understand the shortcut, first we have to divide SOHCAHTOA into three parts as given below.

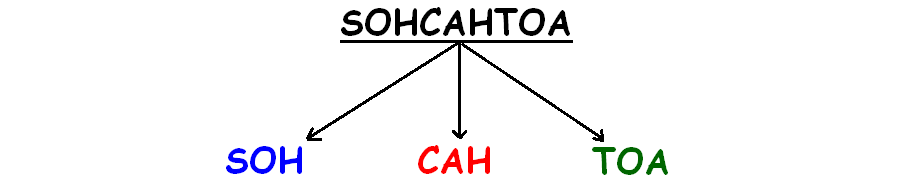
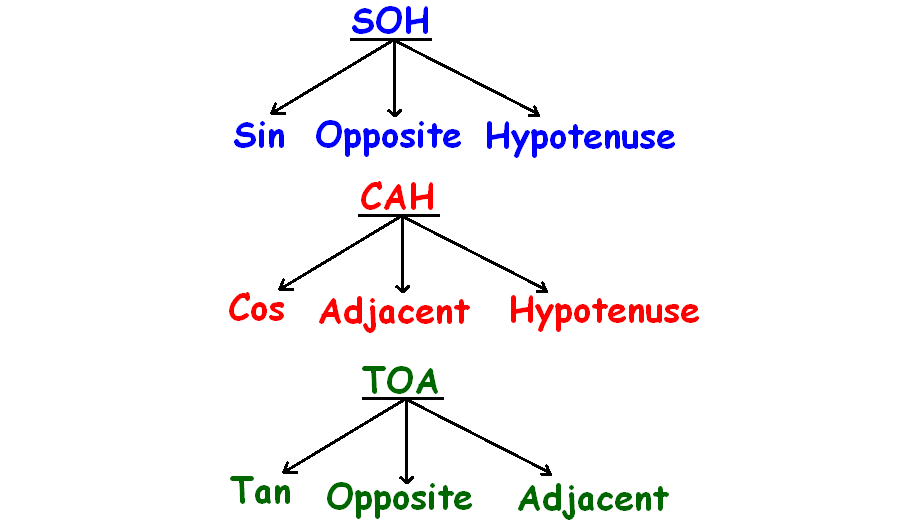
What do SOH, CAH and TOA stand for?

Here is the answer

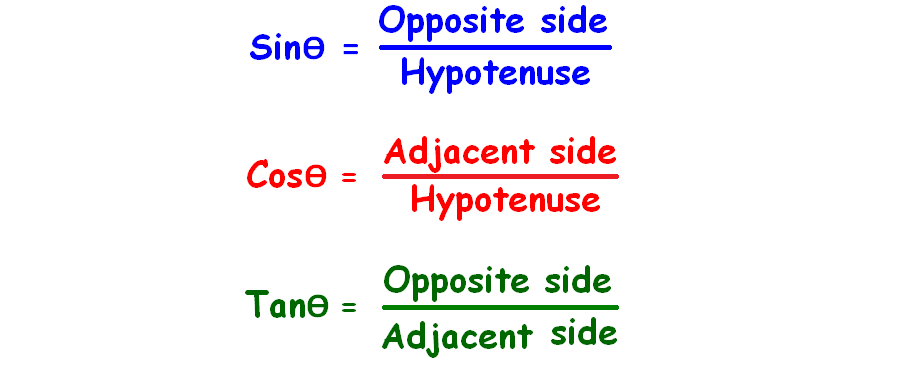
From the above figures, we can derive formulas for the three trigonometric ratios sin, cos and tan as given below.

Reciprocal Relations

The trigonometric ratios cscθ, secθ and cotθ are the reciprocals of sinθ, cosθ and tanθ respectively.

Solved Problems

Problem 1 :

In the right triangle PQR shown below, find the six trigonometric ratios of the angle θ.

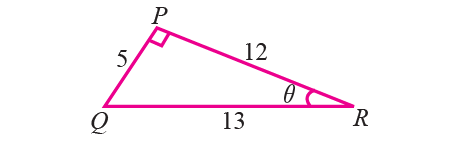
Solution :

In the above right angled triangle, note that for the given angle θ, PQ is the ‘opposite’ side and PR is the ‘adjacent’ side.

Then,

sinθ = opposite side/hypotenuse = PQ/QR = 5/13

cosθ = adjacent side/hypotenuse = PR/QR = 12/13

tanθ = opposite side/adjacent side = PQ/PR = 5/12

cscθ = 1/sinθ = 13/5

secθ = 1/cosθ = 13/12

cotθ = 1/tanθ = 12/5

Problem 2 :

In the figure shown below, find the six trigonometric ratios of the angle θ.

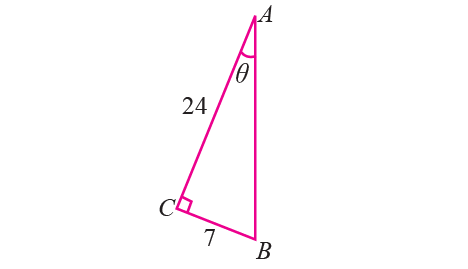
Solution :

In the right angled triangle ABC shown above,

AC = 24

BC = 7

By Pythagorean theorem,

AB² = BC² + CA²

AB² = 7² + 24²

AB² = 49 + 576

AB² = 625

AB² = 25²

AB = 25 

Now, we can use the three sides to find the six trigonometric ratios of angle θ.

sinθ = opposite side/hypotenuse = BC/AB = 7/25

cosθ = adjacent side/hypotenuse = AC/AB = 24/25

tanθ = opposite side/adjacent side = BC/AC = 7/24

cscθ = 1/sinθ = 25/7

secθ = 1/cosθ = 25/24

cotθ = 1/tanθ = 24/7

Problem 3 :

In triangle ABC, right angled at B, 15sin A = 12. Find the other five trigonometric ratios of the angle A.

Solution :

15sinA = 12

sinA = 12/15

sinA = opposite side/hypotenuse

sinA = 12/15

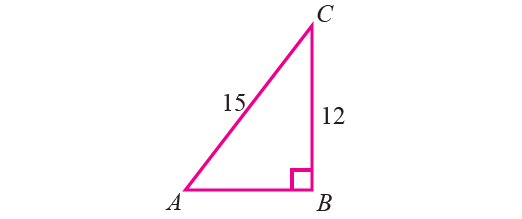
By Pythagorean theorem,

AC² = AB² + BC²

15² = AB² + 12²

225 = AB² + 144

Subtract 144 from each side.

81 = AB²

9² = AB²

9 = AB 

Now, we can use the three sides to find the five trigonometric ratios of angle A and six trigonometric ratios of angle C.

cosA = adjacent side/hypotenuse

= AB/AC

= 9/15

= 3/5

tanA = opposite side/adjacent side

= BC/AB

= 12/9

= 4/3

cscA = 1/sinA

= 15/12

= 5/4

secA = 1/cosA

= 5/3

cotA = 1/tanA

= 3/4

Problem 4 :

In the figure shown below, find the values of

sinB, secB, cotB, cosC, tanC and cscC

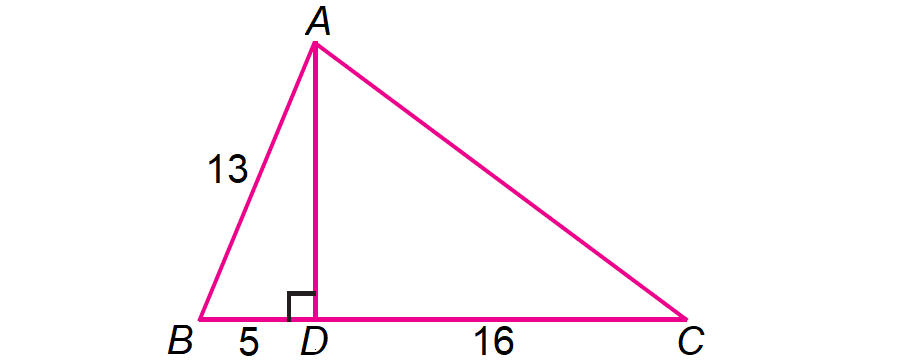
Solution :

In the right ΔABD, by Pythagorean Theorem,

AB² = AD² + BD²

13² = AD² + 5²

169 = AD² + 25

Subtract 25 from each side.

144 = AD²

12² = AD²

12 = AD

In the right ΔACD, by Pythagorean Theorem,

AC² = AD² + CD²

AC² = 12² + 16²

AC² = 144 + 256

AC² = 400

AC² = 20²

AC = 20

Then,

sinB = opposite side/hypotenuse = AD/AB = 12/13

secB = hypotenuse/adjacent side = AB/BD = 13/5

cotB = adjacent side/opposite side = BD/AD = 5/12

cosC =  adjacent side/hypotenuse 

= CD/AC

= 16/20

= 4/5

tanC = opposite side/adjacent side

= AD/CD

= 12/16

= 3/4

cscC = hypotenuse/opposite side

= AC/AD

= 20/12

= 5/3

Problem 5 :

A tower stands vertically on the ground. From a point on the ground, which is 48 m away from the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower.

Solution :

Let PQ be the height of the tower.

Take PQ = h and QR is the distance between the tower and the point R. 

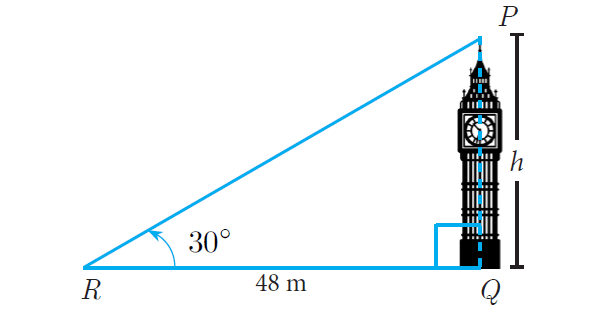
In right triangle PQR above, considering ∠PRQ = 30°, PQ being the opposite side and QR being the adjacent side.

We know the length of the adjacent side (= 48 m) and we have to find the length of the opposite side (height of the tower).  

We know that

tanθ = opposite side/adjacent side

In right triangle PQR,

tan∠PRQ = PQ/QR

tan30° = h/48

From trigonometric ratio table, we have tan30° = √3/3.

√3/3 = h/48

Multiply both sides by 48.

48√3/3 = h

16√3 = h

The height of the tower is 16√3 m.

Problem 6 :

A kite is flying at a height of 75 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.

Solution :

Let AB be the height of the kite above the ground. Then, AB = 75. Let AC be the length of the string.

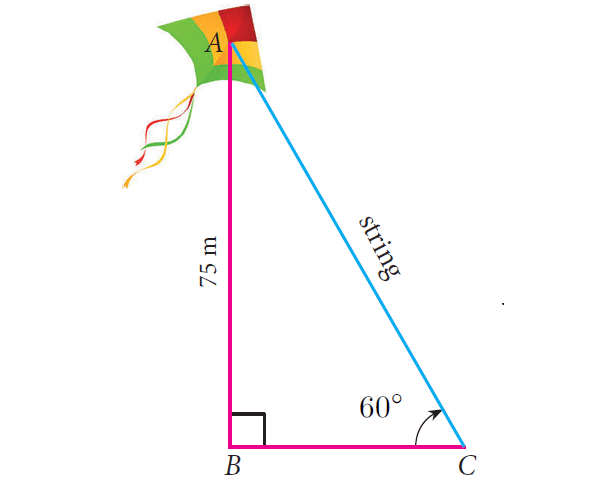
In right triangle ABC above, considering ∠ACB = 60°, AB being the opposite side and AC being the hypotenuse.

We know the length of the opposite side (= 75 m) and we have to find the length of the hypotenuse (length of the string).

We know that

sinθ = opposite side/hypotenuse

In right triangle PQR,

sin∠ACB = AB/AC

sin60° = 75/AC

From trigonometric ratio table, we have sin60° = √3/2.

√3/2 = 75/AC

Take reciprocal on both sides.

2/√3 = AC/75

Multiply both sides by 75.

150/√3 = AC

150√3/3 = AC

50√3 = AC

The length of the string is 50√3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.