TRIGONOMETRIC RATIO TABLE
The table provided in this section will help you to find the values of trigonometric ratios for standard angles 0°, 30°, 45°, 60° and 90°.
The values of trigonometric ratios of standard angles are very important to solve many problems in trigonometry.
Therefore, it is important to remember the values of the trigonometric ratios of these standard angles.
Values of Trigonometric Ratios for Standard Angles
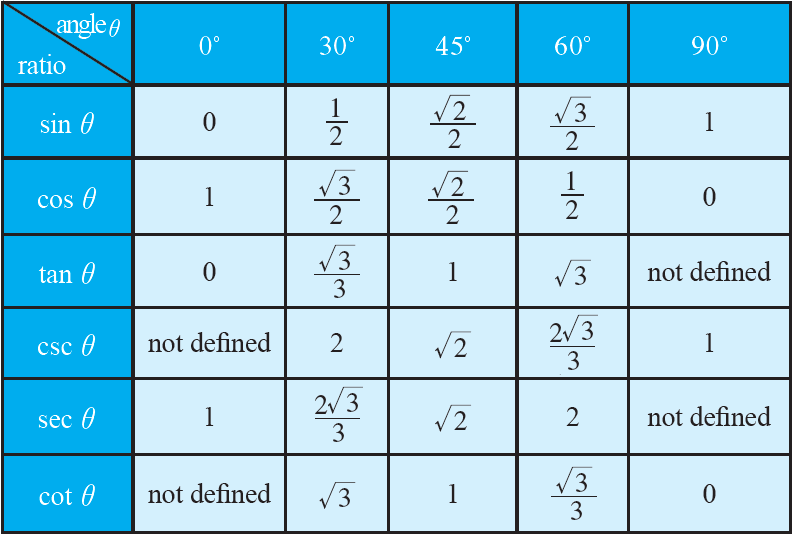
Now, let us see, how the above values of trigonometric ratios are determined for the standard angles.
First, let us see how the values are determined for the angles 30° and 60°
Trigonometric Ratios of 30° and 60°
Let ABC be an equilateral triangle whose sides have length a (see the figure given below). Draw AD perpendicular to BC, then D bisects the side BC.
So, BD = DC = a/2 and < BAD = <DAC = 30°.
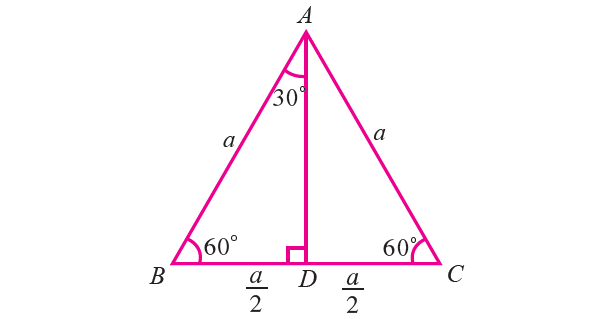
Now, in right triangle ADB, <BAD = 30° and BD = a/2.
In right triangle ADB, by Pythagorean theorem,
AB² = AD² + BD²
a² = AD² + (a/2)²
AD² = a² - (a²/4)
AD² = 3a²/4
AD = √(3a²/4)
AD = √3 x (a/2)
Hence, we can find the trigonometric ratios of angle 30° from the right triangle ADB.
In right triangle ADB, <ABD = 60°. So, we can determine the trigonometric ratios of angle 60°.
Now, let us see how the values are determined for the angle 45°.
Trigonometric Ratios of 45°
If an acute angle of a right triangle is 45°, then the other acute angle is also 45°.
Thus the triangle is isosceles. Let us consider the triangle ABC with <B = 90°, <A = <C = 45°
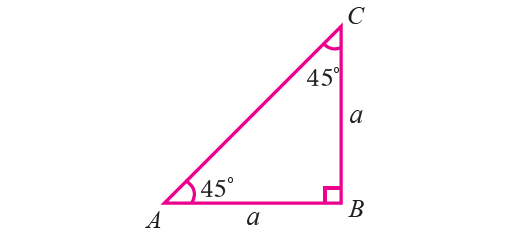
Then AB = BC. Let AB = BC = a.
By Pythagorean theorem,
AC² = AB² + BC²
AC² = a² + a²
AC² = 2a²
AC = √2 x a
Hence, we can find the trigonometric ratios of angle 45° from the right triangle ABC.
Now, let us see how the values are determined for the angles 0° and 90°.
Trigonometric Ratios of 0° and 90°
Consider the figure given below which shows a circle of radius 1 unit centered at the origin.
Let P be a point on the circle in the first quadrant with coordinates (x, y).
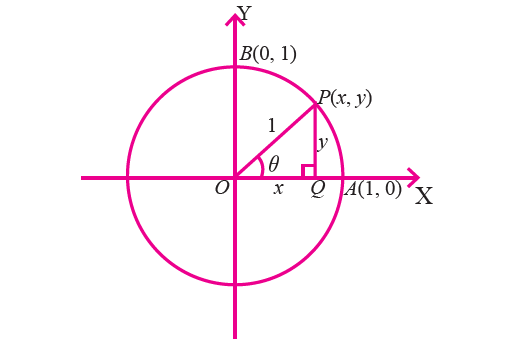
We drop a perpendicular PQ from P to the x-axis in order to form the right triangle OPQ.
Let <POQ = θ, then
sin θ = PQ / OP = y/1 = y (y coordinate of P)
cos θ = OQ / OP = x/1 = x (x coordinate of P)
tan θ = PQ / OQ = y/x
If OP coincides with OA, then angle θ = 0°.
Since, the coordinates of A are (1, 0), we have
If OP coincides with OB, then angle θ = 90°.
Since, the coordinates of B are (0, 1), we have
The six trigonometric ratios of angles 0°, 30°, 45°, 60° and 90° are provided in the following table.
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Powers of Monomials
Oct 20, 20 09:11 PM
Powers of Monomials
-
Properties of Equality Worksheet
Oct 20, 20 12:41 PM
Properties of Equality Worksheet
-
Properties of Equality
Oct 20, 20 12:34 PM
Properties of Equality - Concept - Practice Problems
