LINES OF SYMMETRY

If we can reflect (or flip) a figure over a line and the figure appears unchanged, then the figure has reflection symmetry or line symmetry.

The line that we reflect over is called the line of symmetry.

A line-of symmetry divides a figure into two mirror-image halves.

Some shapes will have no line of symmetry.

Some shapes will have finite lines of symmetry.

Some shapes will have infinite lines of symmetry.

Paper Folding Method

We can imagine the shape given as a paper.

To check the line of symmetry, we have to fold the paper through the line.

If the shapes on both sides of the line get matched, then the line through which the paper is folded can be considered as line of symmetry.

If the shapes on both sides of the line do not get matched, then the line through which the paper is folded can not be considered as line of symmetry.

Paper Folding Method Examples

Example 1 :

Is the dotted line on the shape given below a line of symmetry?

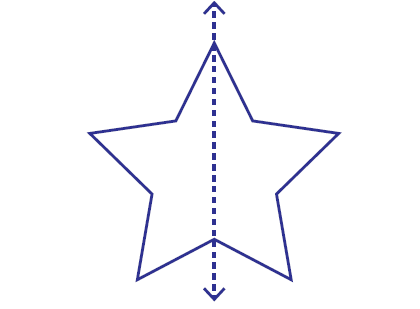
Answer : Yes

Explanation :

We can imagine the above shape given as a paper. If we fold the paper through the dotted line, transparently the shapes on both the sides of the line get matched.

So, the dotted line is line of symmetry.

Example 2 :

Is the dotted line on the shape given below a line of symmetry?

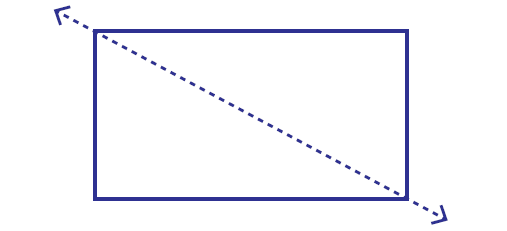
Answer : No

Explanation :

We can imagine the above shape given as a paper. If we fold the paper through the dotted line, transparently the shapes on both the sides of the line do not get matched.

So, the dotted line is not line of symmetry.

Example 3 :

Is the dotted line on the shape given below a line of symmetry?

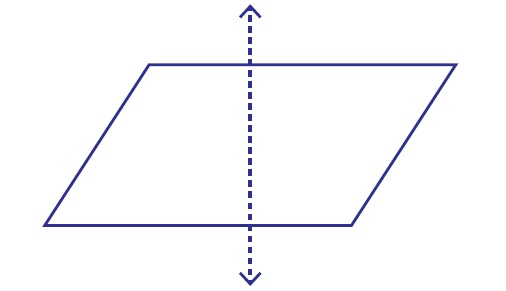
Answer : No

Explanation :

We can imagine the above shape given as a paper. If we fold the paper through the dotted line, transparently the shapes on both the sides of the line do not get matched.

So, the dotted line is not line of symmetry.

Example 4 :

Is the dotted line on the shape given below a line of symmetry?

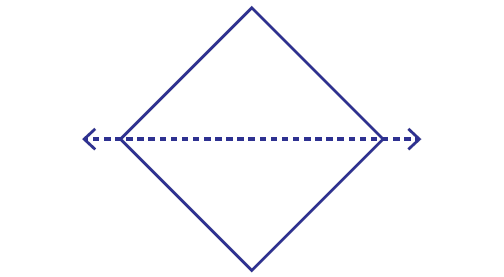
Answer : Yes

Explanation :

We can imagine the above shape given as a paper. If we fold the paper through the dotted line, transparently the shapes on both the sides of the line get matched.

So, the dotted line is line of symmetry.

Example 5 :

Is the dotted line on the shape given below a line of symmetry ?

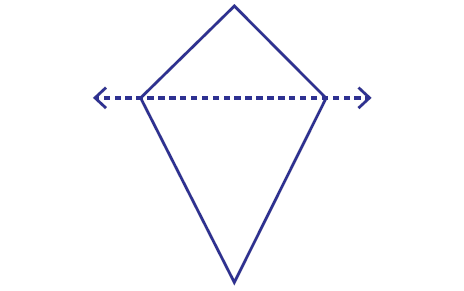
Answer : No

Explanation :

We can imagine the above shape given as a paper. If we fold the paper through the dotted line, transparently the shapes on both the sides of the line do not get matched.

So, the dotted line is not line of symmetry.

Example 6 :

Is the dotted line on the shape given below a line of symmetry ?

Answer : Yes

Explanation :

We can imagine the above shape given as a paper. If we fold the paper through the dotted line, transparently the shapes on both the sides of the line get matched.

So, the dotted line is line of symmetry.

Example 7 :

Is the dotted line on the shape given below a line of symmetry ?

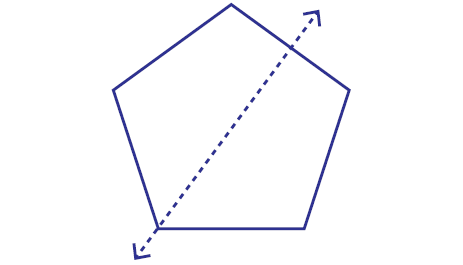
Answer : Yes

Explanation :

We can imagine the above shape given as a paper. If we fold the paper through the dotted line, transparently the shapes on both the sides of the line get matched.

So, the dotted line is line of symmetry.

Example 8 :

Is the dotted line on the shape given below a line of symmetry ?

Answer : No

Explanation :

We can imagine the above shape given as a paper. If we fold the paper through the dotted line, transparently the shapes on both the sides of the line do not get matched.

So, the dotted line is not line of symmetry.

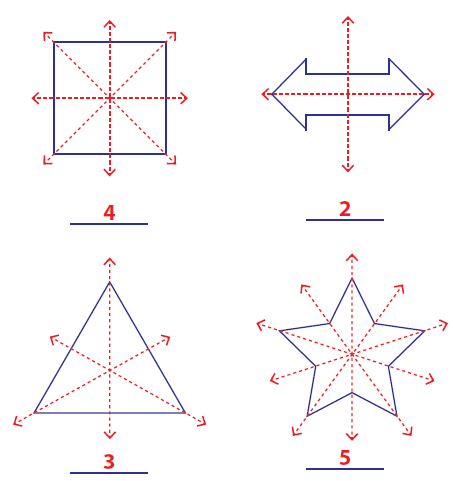
Counting Number of Lines of Symmetry

Draw line of symmetry on each shape. Count and write the lines of symmetry.

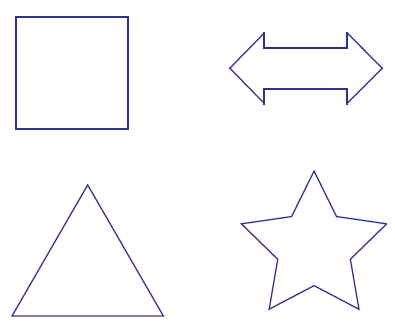
Based on the paper folding method explained above, we can draw the lines of symmetry as given below.

Line of Symmetry - Alphabets

Line of symmetry in letters of the English alphabet :

Letters having one line of symmetry :

A,  B, C, D, E, K, M, T, U, V, W, Y

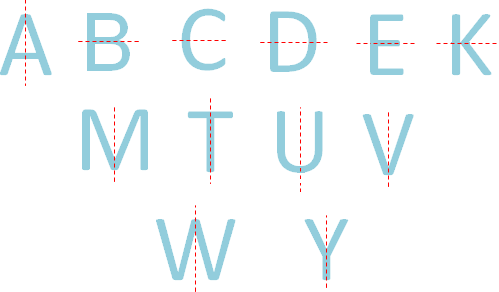
From the above picture, we can have the following two points.

A M T U V W Y have vertical line of symmetry.

B C D E K  have horizontal line of symmetry.

Letters having two lines of symmetry :

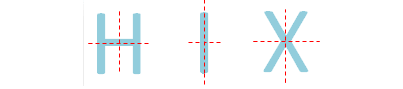
From the above picture,

H, I, X

have  both horizontal and vertical lines of symmetry.

Letters having no line of symmetry :

F,  G, J, L, N, P, Q, R, S, Z

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.