SAT MATH QUESTIONS ON LINES

Question 1 :

In the xy-plane, the following two lines are parallel.

y = mx - 5

2x + 3y = 6

Find the value of m.

Answer :

The equation of the first line y = mx - 5 is in slope- intercept form and its slope is 'm'

Write the equation of the second line 2x + 3y = 6 in slope-intercept for, that is y = mx + b.

2x + 3y = 6

Subtract 2x from both sides.

3y = -2x + 6

Divide both sides by 3.

3y/3 = -2x/3 + 6/3

y = -2x/3 + 2

Comparing y = -2x/3 + 2 with y = mx + b, m = -2/3.

Since the lines are parallel, slopes are equal.

slope of the 1^st line = slope of the 2^nd line

m = -2/3

Question 2 :

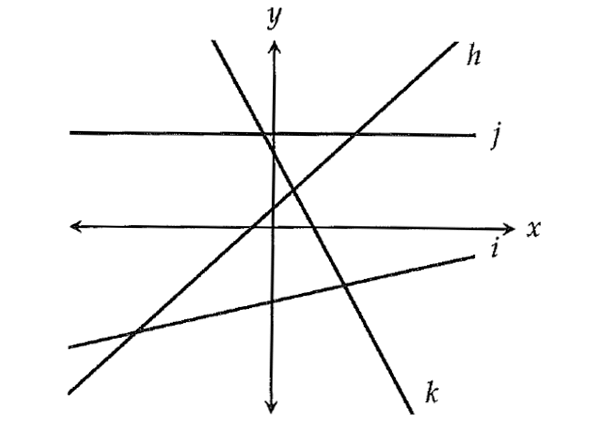
In the figure above, lines h, i, j and k are graphed in the xy-plane. Which of the following correctly orders than by their slope from least to greatest?

A) k < j < i < h

B) k < i < j < h

C) k < j < h < i

D) j < k < i < h

Answer :

In the figure above, k is a falling line.

slope of k is negative ----(1)

The lines h, i and j are raising lines, hence their slopes are positive.

Line h is steeper than the line i.

slope of i < slope of h ----(2)

Line i is steeper than the line j.

slope of j < slope of i ----(2)

Comparing (1), (2) and (30,

slope of k < slope of j < slope of i < slope of h

The correct answer choice is (A).

Question 3 :

In the xy-plane above, the line y = mx + b, where m is the slope and b is the y-intercept, is a reflection of a line across the y-axis. At which of the following points do the two lines intersect?

A) (0, b)

B) (0, -b)

C) (0, m)

D) (m , 0)

Answer :

A line and its reflection across the y-axis intersect at the y-intercept. For the given line y = mx + b, the y-intercept is b or (0, b).

Therefore, (0, b) is the point at which the two lines intersect.

The correct answer choice is (A).

Question 4 :

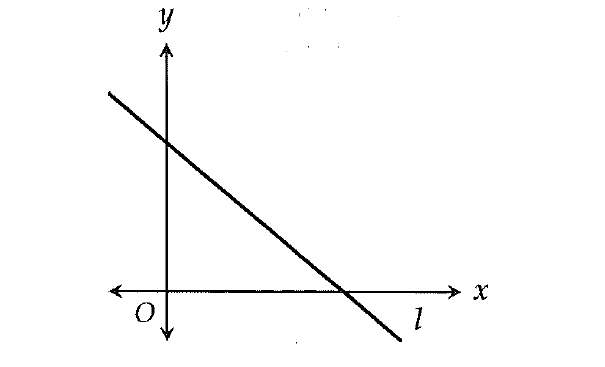
The graph of line ℓ is shown in the xy-plane above. The equation of line n (not shown) is y = mx + b, where m and b are constants. If line ℓ is perpendicular to line n, which of the following must be true?

A) m < 0

B) m > 0

C) b < 0

D) b > 0

Answer :

Draw two possible lines which are perpendicular to the given line ℓ. 

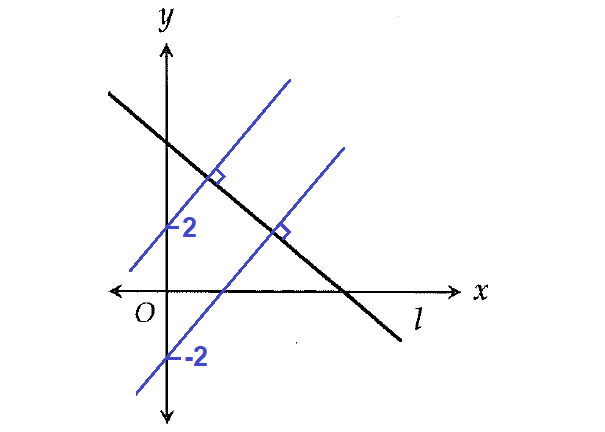
From the graph above, it is clear that the line n (perpendicular to line ℓ) may have positive y-intercept or negative y-intercept.

Given : Equation of the line n is y = mx + b.

So, the value of the y-intercept of 'b' in y = mx + b may be positive or negative and we can not predict exactly as

b > 0 or b < 0

Hence, we can reject options (C) and (D).

If two lines are perpendicular, the product of their slopes is equal to -1. Since the product of the slopes is a negative value, one line has a positive slope and the other line has a negative slope.

The line k shown in the xy-plane above is a falling line, so it has a negative slope.

Then, the other line n (not shown) perpendicular to line k must have a positive slope.

Slope of the line y = mx + b is 'm' and it is positive.

That is

m > 0

The correct answer choice is (B).

Question 5 :

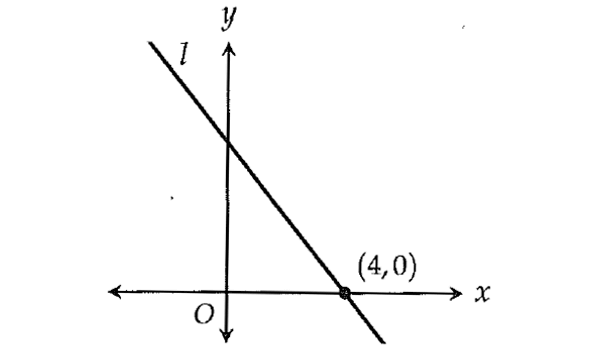
In the xy-plane above, the line l has slope -5/4. What is the area of the triangle bounded by line l, the x-axis and the y-axis?

Answer :

slope = -5/4

rise/run = -5/4

rise ---> 5 units down

run ----> 4 units to the right

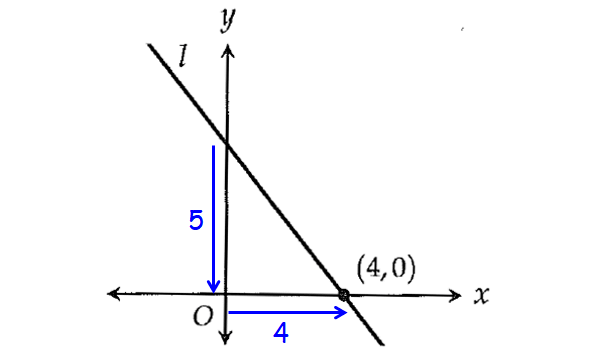
Clearly, the base of the triangle is 4 and the height is 5.

Formula for area of a triangle :

= (1/2) ⋅ b ⋅ h

Substitute b = 4 and h = 5.

= (1/2) ⋅ 4 ⋅ 5

= 20/2

= 10 square units

Question 6 :

In the xy-plane above, the line with equation 3x + 4y = 6 is perpendicular to the line with equation y = mx + b, where m and b are constants. What is the value of m?

Answer :

The slope of the line y = mx + b is 'm'.

Write the equation 3x + 4y = 6 in slope-intercept form.

3x + 4y = 6

Subtract 3x from both sides.

4y = -3x + 6

Divide both sides by 4.

4y/4 = -3x/4 + 6/4

y = -3x/4 + 3/2

The equation of the line y = -3x/4 + 3/2 is in slope intercept form, that is y = mx + b.

Slope of the line y = -3x/4 + 3/2 is

m = -3/4

Given : The line with equation 3x + 4y = 6 is perpendicular to the line with equation y = mx + b.

If two lines are perpendicular to each other, the product of their slopes is equal to -1.

(-3/4) ⋅ m = -1

-3m/4 = -1

Multiply both sides by 4.

-3m = -4

Divide both sides by -3.

m = -4/3

Question 7 :

If a line contains the points (0, 0) and (12, 16), then the line will also contain which of the following points?

A) (2, 3)

B) (3, 2)

C) (3, 4)

D) (4, 3)

Answer :

Find the slope of the line joining (0, 0) and (12, 16),

Slope of the line joining (x₁, y₁) and (x₂, y₂) ;

m = (y₂ - y₁)/(x₂ - x₁)

Substitute (x₁, y₁) = (0, 0) and (x₂, y₂) = (12, 16).

m = (16 - 0)/(12 - 0)

m = 16/12

m = 4/3

Equation of the line in slope-intercept form :

y = mx + b

Substitute m = 4/3.

y = 4x/3 + b

Since, the line is passing through the origin (0, 0), y-intercept b = 0.

Then, the equation of the line is y = 4x/3.

To find the point the line contains, check each point in the given options with the equation

y = 4x/3

A) (2, 3) :

3 = 4(2)/3

3 = 8/3  ✘

B) (3, 2) :

2 = 4(3)/3

3 = 12/3

3 = 4  ✘

C) (3, 4) :

4 = 4(3)/3

4 = 12/3

  4 = 4  ✔

D) (4, 3) :

3 = 4(4)/3

3 = 16/3

3 = 16/3  ✘

The correct answer choice is (C).

Question 8 :

If m and b are real numbers and m > 0 and b > 0, then the line whose equation is y = mx + b can not contain which of the following points?

A) (0, 1)

B) (1, 1)

C) (-1, 1)

D) (0, -1)

Answer :

For the given line y = mx + b,

slope = m

y-intercept = b

It is given that m > 0 and b > 0.

Since the y-intercept b is positive, the line intersects y-axis at a positive point and it will never intersect the y-axis at a negative point. 

In the given answer choices, (D) (0, -1) contains a negative point on the y-axis.

So, the line y = mx + b can not contain the point (0, -1).

The correct answer choice is (D).

Question 9 :

If a line has positive slope and positive y-intercept, then which of the following points the line can not contain?

A) (-1, 4)

B) (2, 3)

C) (1, -5)

D) (1, -4)

Answer :

The slope of the line is positive, so it is a raising line.

Since the y-intercept b is positive, the line intersects y-axis at a positive point. 

Graph of the line :

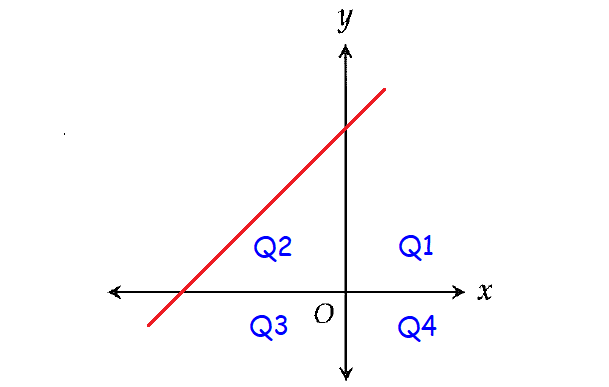
The line passes through the quadrants Q1, Q2 and Q3 and it does not pass through the quadrant 4.

In the given answer choices, (C) (1, -5) contains a point in quadrant 4.

So, the line can not contain the point (1, -5), because it is in quadrant 4.

The correct answer choice is (C).

Question 10 :

A line with the equation y = 2x - b passes through the point (2b, -9), what is the value of b?

Answer :

y = 2x - b

Since the line passes through the point (2b, -9), we can plug in x = 2b and y = -9 into the equation.

-9 = 2(2b) - b

-9 = 4b - b

-9 = 3b

Divide both sides by 3.

-3 = b

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.