HARDEST SAT MATH QUESTIONS (Part - 4)

Question 1 :

2x² + 7x - 15  =  0

If r and s are two solutions of the equation above and r > s, which of the is the value of r - s?

(A) 15/2           (B) 13/2           (C) 11/2           (D) 3/2

Answer : 

2x² + 7x - 15  =  0

Factor and solve : 

Multiply the coefficient of x², that is 2 and the constant -15. The result is -30. Find two factors for -30 such that the product is -30 and sum is equal to the coefficient of x, that is +7. Then, the two factors are +10 and -3.

2x² + 10x - 3x - 15  =  0

2x(x + 5) - 3(x + 5)  =  0

2x(x + 5) - 3(x + 5)  =  0

(x + 5)(2x - 3)  =  0

The two solutions of the given quadratic equation are -5 and 3/2.

It is given that r and s are the two solutions of the given quadratic equation such that r > s.

Then, r = 3/2 and s = -5. 

r - s  =  3/2 - (-5)

=  3/2 + 5

=  13/2

The correct answer is (B). 

Question 2 :

A parachute design uses 18 separate pieces of rope. Each piece of rope must be at least 270 centimeters and no more than 280 centimeters long. What inequality represents all possible values of the total length of rope x, in centimeters, needed for the parachute?

A) 270 ≤ x ≤ 280

B) 4,860 ≤ x ≤ 4,870

C) 4,860 ≤ x ≤ 5,040

D) 5,030 ≤ x ≤ 5,040

Answer : 

The total length of all 18 separate pieces of rope is x. 

It is given that the minimum length each piece of rope is 270 cm and the maximum length  is 280 cm.

270 ≤ x ≤ 280

Then, the inequality represents all possible values of the total length of all 18 pieces : 

270(18) ≤ x ≤ 280(18)

4860 ≤ x ≤ 5040

The correct answer is (C). 

Question 3 :

A carpenter has $60 with which to buy supplies. The carpenter needs to buy both nails and screws. Nails cost $12.99 per box, and screws cost $14.99 per box. If n represents the number of boxes of nails and s represents the number of boxes of screws, which of the following systems of inequalities models this situation?

A)  12.99n + 14.99s ≥ 60
       n + s ≤ 1

B) 12.99n + 14.99s ≤ 60
     n + s ≤ 1

C) 12.99n + 14.99s ≥ 60
      n ≥ 1
      s ≥ 1

D) 12.99n + 14.99s ≤ 60
      n ≥ 1
      s ≥ 1

Answer : 

n ----> number of boxes of nails

s ----> number of boxes of screws

A box of nails costs $12.99 per box and a box of screws costs $14.99. 

Total cost of n boxes of nails and s boxes of screws is 

12.99n + 14.99

Since the carpenter has $60, the total cost can be equal to $60 or less than that.

12.99n + 14.99 ≤ 60

Also, the carpenter has to buy both nail and screw, thus, at least 1 box of nail and 1 box of screw must be purchased.

n ≥ 1 and s ≥ 1

The correct answer is (D).

Question 4 :

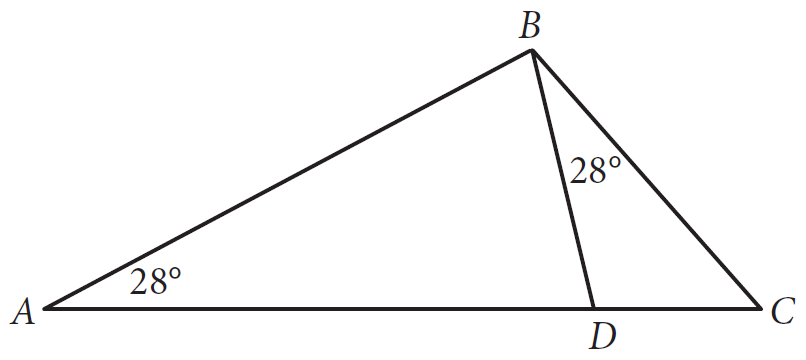
In the figure above, which of the following ratios has the same value as AB/BC ?

(A) BD/DC       (B) BC/AC       (C) AD/BD       (D) DC/BC

Answer : 

We can separate the two triangles shown below. 

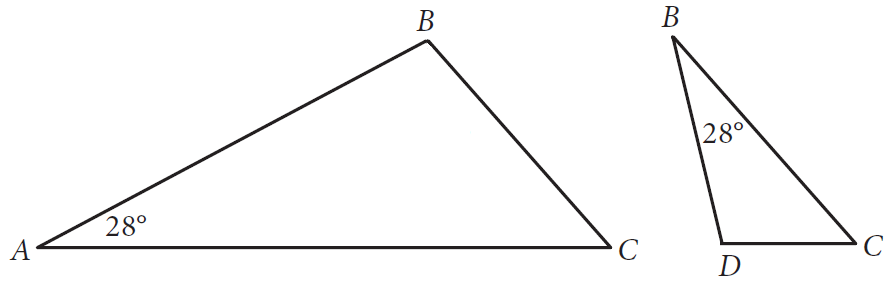
In the above two triangles, 

m∠C  =  m∠C (common angle)

m∠A  =  m∠B  =  28°

By AA Similarity Postulate, ΔABC and ΔBDC are similar. 

So the corresponding sides are proportional. 

AB/BD  =  BC/DC  =  AC/BC

Let's take the first two ratios in the above proportion. 

AB/BD  =  BC/DC

AB/BC  =  BD/DC

The correct answer is (A).

Question 5 :

p(x)  =  3(x² + 10x + 5) - 5(x - k)

In the polynomial p(x) defined above, k is a value constant. If p(x) is divisible by x, what is the value of k ?

(A) -3               (B) -2               (C) 0               (D) 3

Answer : 

p(x) is divisible by x ----> x is a factor p(x)

It is clear that p(x) = 0, when x = 0. That is, 

p(0)  =  0

3(0² + 10(0) + 5) - 5(0 - k)  =  0

3(0 + 0 + 5) - 5(-k)  =  0

3(5) - 5(-k)  =  0

15 + 5k  =  0

5k  =  -15

k  =  -3

The correct answer is (A).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.