HARDEST SAT MATH QUESTIONS (Part - 1)

Question : 1

The equation above shows how temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true?

I. A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 59 degrees Celsius.

II. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.

III. A temperature increase of 5/9 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.

A. I only

B. II only

C. III only

D. I and II only

Answer :

Solve the above equation for F in terms of C.

Statement I :

A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 5/9 degrees Celsius.

In (1), if F = 0,

C = (5/9)(0) - 160/9

C = 0 - 160/9

C = -160/9

If F = 1

C = (5/9)(1) - 160/9

C = 5/9 - 160/9

C = - 160/9 + 5/9

Statement I is correct.

Statement II :

A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.

In (2), if C = 0,

F = (9/5)(0) + 32

F = 0 + 32

F = 32

If C = 1

F = (9/5)(1) + 32

F = 1.8 + 32

F = 32 + 1.8

Statement II is correct.

Statement III :

A temperature increase of 5/9 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.

In (1), if F = 0,

C = (5/9)(0) - 160/9

C = 0 - 160/9

C = -160/9

If F = 5/9

C = (5/9)(5/9) - 160/9

C = 25/81 - 160/9

C = -160/9 + 25/81

A temperature increase of 5/9 degree Fahrenheit is equivalent to a temperature increase of 25/81 degree Celsius, NOT 1 degree Celsius.

Statement III is incorrect.

The correct answer choice is (D).

Question 2 :

An office building has a room with a square-shaped floor. The actual length of the floor is 90 times the length of the floor on a blueprint drawn to scale. The actual area of the floor is p times the area of the floor on the blueprint. Find the value of p.

Answer :

Length :

Let 'x' be the length of each side of the square-shaped floor in blue print. 

Then, the actual length of the floor is 90x.

Area :

Area of the square-shaped floor in blueprint is x². 

Then, the actual area of the floor  =  px² ----(1). 

Since the actual length of the floor is 90x, the area of the floor is 

=  (90x)²

=  90²x²

=  8100x² ----(2)

Both (1) and (2) represent the actual area of the floor. 

Then, 

px²  =  8100x²

Divide each side by x².

p  =  8100

Question 3 :

The equation given below is true for all values of x ≠ 2/a, where a is a constant. What is the value of a ?

Answer :

Multiply each side by (ax - 2). 

24x² + 25x - 47  =  (ax - 2)(-8x - 3) - 53

24x² + 25x - 47  =  -8ax² - 3ax + 16x + 6 - 53

24x² + 25x - 47  =  -8ax² + 16x - 3ax - 47

24x² + 25x - 47  =  -8ax² + (16 - 3a)x - 47

On the both sides of the above equation, we have quadratic expressions. 

If two expressions are equal, then the coefficients of like terms are also equal. 

The, equate the coefficients of x².

-8a  =  24

Divide each side by -8. 

a  =  -3

Question 4 :

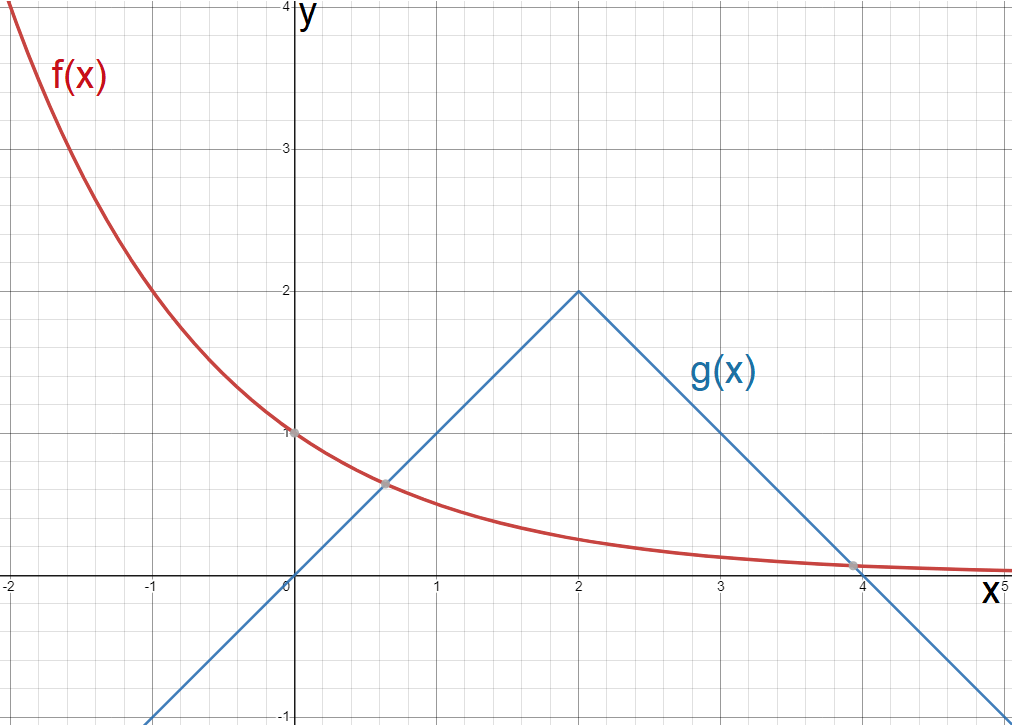
The functions f(x) and g(x) are graphed in the xy-plane above. Based on the graph, what are the solutions to the equation when f(x) = g(x) ?

(A) The x-intercepts

(B) The y-intercepts

(C) The x-values of the points of intersection. 

(D) The y-values of the points of intersection.

Answer :

In the above graph, both f(x) and g(x) represent the y-coordinate of each function. 

So, f(x) = g(x) is similar to y = y. 

When we solve the equations of two curves, we get the x and y coordinates of the point of intersection as solution.

Here, we solve f(x) and g(x) by equating them, that is

f(x) = g(x)  or  y = y

In y = y, we will be substituting some stuff for each y in terms of x.

Then, the solution for the above equation is x-values of the points of intersection.

The correct answer choice is (C). 

Question 5 :

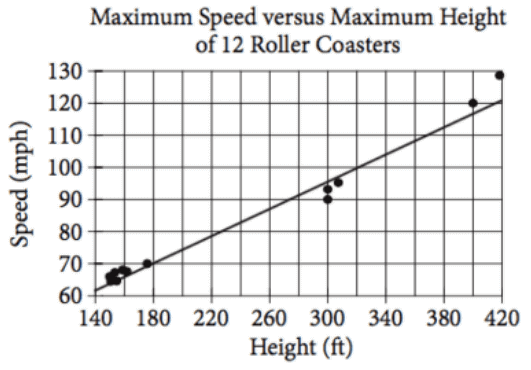
The scatterplot above shows the maximum height h, in feet (ft), and maximum speed s, in miles per hour (mph), of 12 roller coasters as well as the line of best fit for the data. Of the following, which best represents an equation for the line of best fit?

(A) s = 0.21h + 32     (B) s = 0.43h + 32

(C) s = 0.21h + 62     (D) s = 0.43h + 62

Answer :

In the above graph, it is clear that the y-intercept (speed) is about 62. So, we can reject options (A) and (B).

To know the slope of the line of best fit, mark two points and use rise-over-run formula. 

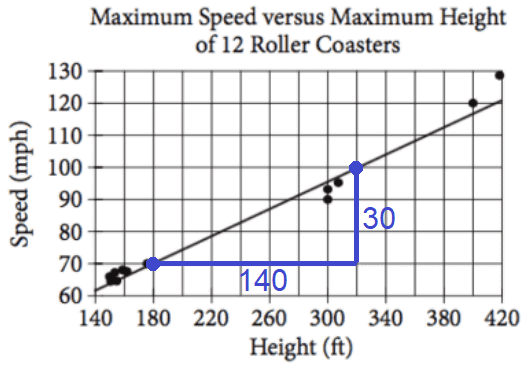
In the graph above, 

rise  =  30

run  =  140

Slope  =  rise / run

=  30/140

≈  0.21

So, the equation of line of best fit is

s  =  0.21h + 62

The correct answer choice is (C). 

Question 6 :

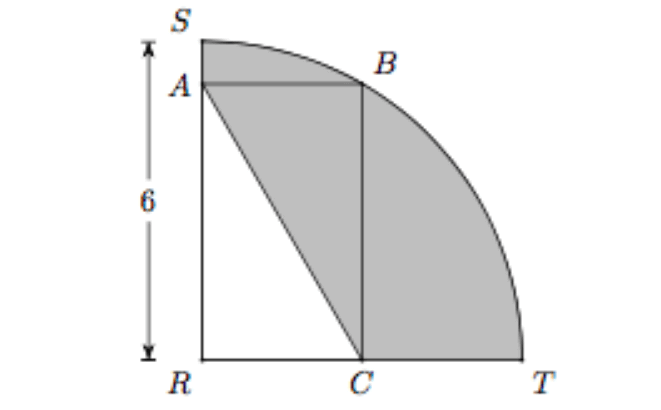
In the figure above, arc SBT is one quarter of a circle with center R and radius 6. If the length plus the width of rectangle ABCR is 8, Then the perimeter of the shaded region is

(A)  8 + π    (B)  10 + 3π

(C) 14 + 3π    (D)  8 + π

Answer :

Idea to solve this problem : 

Find the perimeter of one quarter of the circle STR. Subtract the length (AR) and width (RC) of the rectangle ABCR from the above perimeter. Then, add the  the length of the diagonal (AC).  

Step 1 :

Perimeter of one quarter of the circle STR is

=  2πr/4 + 2r

=  πr/2 + 2r

Substitute 6 for r. 

=  6π/2 + 2(6)

=  3π + 12

Step 2 :

Given : The length plus width of rectangle ABCR is 8.

Then, 

AR + RC  =  8

Subtract 8 from the perimeter found in step 1. 

=  3π + 12 - 8

=  3π + 4

Step 3 : 

The two diagonals of the rectangle ABCR are AC and RB in which RB is being as radius of the circle. 

So, RB = 6.

In any rectangle, the lengths of two diagonals are always congruent. 

Then, AC = 6. 

Add the length of the diagonal AC (= 6) to the result of step 2.

=  3π + 4 + 6

=  3π + 10

Perimeter of the shaded region is (10 + 3π).

The correct answer choice is (B).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.