HARDEST SAT MATH QUESTIONS (Part - 2)

Question 1 :

P  =  215(1.005)^t/3

The equation above can be used to model the population, in thousands, of a certain city t years after 2000. according to the model, the population is predicted to increase by 0.5% every n months. what is the value of n ?

(A) 3     (B) 4     (C) 12     (D) 36

Answer : 

0.5%  = 0.5/100  =  0.005

It is given that the population (215) is predicted to increase by 0.5%. To know the value after increment, 215 has to be multiplied by (1 + 0.005) or 1.005. 

In the equation P  =  215(1.005)^t/3, the value of t/3 has to be equal to 1 for 0.5% increase.

t/3  =  1

t  =  3 years

Convert years to months. 

n  =  3 ⋅ 12 months

n  =  36 months

The correct option is D.

Question 2 :

In the xy-plane, the graph of a linear equation of the form y = mx + b and the graph of an exponential equation of the form y = ab^x both contain points (1, 3) and (2, 4). If the point (r, s) is on the graph of the linear equation and the point (r, t) is on the graph of the exponential equation, where 0 < r < 4 and s > t, which of the following must be true?

(A) 0 < r < 1  (B) 1 < r < 2  (C) 2 < r < 3  (D) 3 < r < 4

Answer : 

Linear equation y = mx + b contains (1, 3) and (2, 4).

Solving (1) and (2), we get 

m  =  1 and b  =  2

Linear equation : y = x + 2. 

Exponential equation y = ab^x contains (1, 3) and (2, 4).

Divide (4) by (3).

ab²/ab¹  =  4/3

b  =  4/3

Substitute b = 4/3 in (3). 

3  =  a(4/3)

Multiply each side by 4/3. 

9/4  =  a

Exponential equation : y = (9/4)(4/3)^x.

Graph the linear and exponential equations :

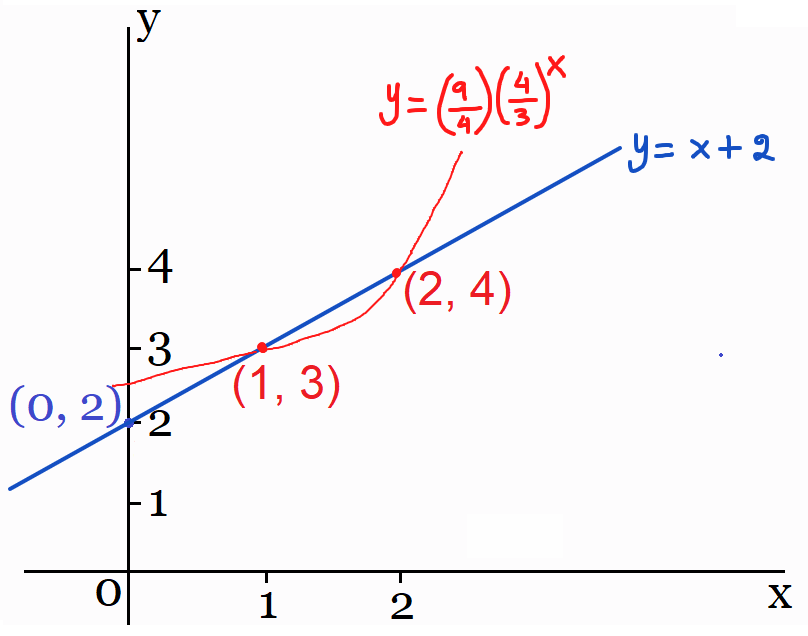
(r, s) is on the graph of the linear equation and the point (r, t) is on the graph of the exponential equation. 

'r' is the x-coordinate in both linear and exponential equations, 's' is the y-co-ordinate in linear equation and 't' is the y-coordinate in exponential equation. 

Given : 0 < r < 4 and s > t

s > t ---> y-coordinate in the linear equation is greater than the y-coordinate in the exponential equation.

In the above graph, the line is above the curve between the x-values 1 and 2.

That is, y-coordinate 's' of the linear equation is greater than the y-coordinate 't' of the exponential equation between the x-values 1 and 2. 

That is, 

1 < r < 2 

The correct option is (B).

Question 3 :

In the xy-plane, the line defined by the equation y = 3x - 5 passes through the vertex of a parabola with x-intercepts of 3 and 15. What is the y-coordinate of the vertex of the parabola ?

Answer : 

x-coordinate of the vertex of a parabola is the average of two x-intercepts.

The average of two x-intercepts 3 and 15 :

=  (3 + 15)/2

=  18/2

=  9

So, x-coordinate of the vertex is 9.

Let 'k' be the y-coordinate of the vertex.

Then, the vertex of the parabola is (9, k). 

The line y = 3x - 5 is passing through the vertex  of the parabola (9, k). 

k  =  3(9) - 5

k  =  27 - 5

k  =  22

So, y-coordinate of the vertex of the parabola is 22.

Question 4 :

The graph of y = f(x - 4) is shown below. For which value of x, must f(x) = 1 ?

Answer : 

We know that the graph of the function y = f(x) has been shifted 4 units to the right to obtain the graph of

y = f(x - 4)

Hence, we can shift the graph of y = f(x - 4) to the left 4 units to obtain the graph y = f(x). 

The graph of y = f(x) is shown below. 

In the above graph, f(x) = 1 (that is, y = 1), when x = 0. 

Question 5 :

Darcy keeps $5,000 in a bank account that does not earn any interest. Every week, she withdraws 10 percent of the money in the account for spending. To the nearest cent, how much has she withdrawn in total after 8 weeks ?

(A) $2610.78  (B) $2638.08  (C) $2755.28  (D) $2847.66

Answer : 

Because Darcy withdraws 10% of the money in the account every week, this problem comes under the concept of compound interest.

Because the money in the account is decaying every week, the compound interest formula can be used with negative sign as shown below. 

A  =  P(1 - r)ⁿ

P ----> Initial deposit

A ----> Final value of the deposit after 'n' weeks

r ---> Percent of decay

Substitute the values in the above formula.

A  =  5000(1 - 0.1)⁸

A  =  5000(0.9)⁸

A  =  5000(0.43046721)

A  ≈  2152.34

The account balance after 8 weeks is about $2152.34.

Amount of money she has withdrawn in total after 8 weeks : 

=  $5000 - $2152.34

=  $2847.66

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.