SAT MATH QUESTIONS ON INEQUALITIES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
Ashley estimates that there are a marbles in a jar. Harry, who knows the actual number of marbles in the jar, b notes that Ashley's estimate is within 15 marbles (inclusive) of the actual number of marbles. Which of the following inequalities represents the relationship between Ashley's estimate and the actual number marbles in the jar?
A) -15 ≤ a - b ≤ 15
B) a ≤ b + 15
C) a ≥ b - 15
D) a + b ≥ 15
Answer :
Ashley's estimation = a
Actual number of marbles = b
Ashley's estimate is within 15 marbles (inclusive) of the actual number of marbles.
The maximum value of Ashley's estimation = b + 15
The minimum value of Ashley's estimation = b - 15
Ashley's estimation 'a' can be any value between (b - 15) and (b + 15) inclusive.
b - 15 ≤ a ≤ b + 15
Subtract b from each value in the inequality.
15 ≤ a - b ≤ 15
The correct answer choice is (A).
Question 2 :
A school district wants to make at least 600 but no more than 700 computers available to students. To meet this goal, the superintendent puts aside a budget to install 8 new computers every month. If there is a total of 200 computers available at the schools in the district currently, which of the following inequalities gives the possible number of months t for which the school district can continue to add new computers? Assume t is an integer.
A) 50 ≤ t ≤ 62
B) 50 ≤ t ≤ 63
C) 75 ≤ t ≤ 87
D) 75 ≤ t ≤ 88
Answer :
A total of 200 computers available at the schools in the district currently, and 8 new computers will be installed every month for t months from now.
Total number of computers after t months :
= 200 + 8t
The minimum value of (200 + 8t) is 600 and maximum value is 700.
600 ≤ 200 + 8t ≤ 700
Subtract 200 from each value.
400 ≤ 8t ≤ 500
Divide each value by 8.
50 ≤ t ≤ 62.5
Because t is an integer,
50 ≤ t ≤ 62
The correct answer choice is (A).
Question 3 :
At a kitchen equipment store, the price of pots is $14 and the price of pans is $10. If Amy spends more than $100 but less than $150 to buy 3 pots and x pans, which of the following is NOT a possible value of x?
A) 6
B) 8
C) 10
D) 12
Answer :
The total amount Amy spends :
= 3(14) + 10x
= 42 + 10x
The total amount (42 + 10x) is greater than 100, but less than 150.
100 < 42 + 10x < 150
Subtract 42 from each value.
58 < 10x < 108
Divide each value by 10.
5.8 < x < 10.8
Of the given answer choices, 12 is the only one that falls outside of this range.
The correct answer choice is (D).
Question 4 :
Lawyers John and Will review legal documents. John charges an initial consultation fee and then $50 for each hour of legal review. Will does not charge a consultation fee but charges $75 for each hour of legal review. The graph below shows the two lawyers' wages, where h is the number of hours worked and y is the total wage in dollars.
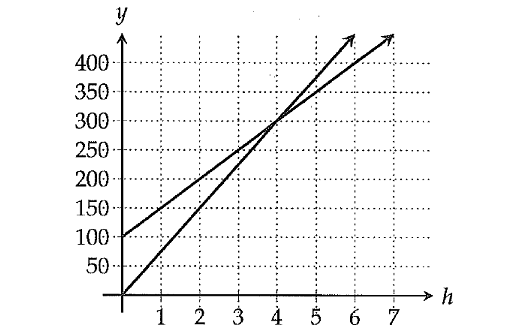
Which of the following inequalities gives all the values of h for which it is less expensive to hire John than it is to hire Will for legal review?
A) h ≥ 0
B) h > 4
C) 0 ≤ h < 4
D) h > 300
Answer :
In the graph above, one line starts at (0, 100) and the other line starts at (0, 0).
(0, 100) ----> h = 0 and y = 100 ---> Initial cost $100
(0, 0) ----> h = 0 and y = 0 ----> No initial cost
Clearly the line starts at (0, 100) has initial cost of $100 and it represents the cost of John and the other line starts at (0, 0) represents the cost of Will.
John's line is below Will's line after h = 4.
Therefore, it is less expensive to hire John when the work is more than 4 hours, h > 4.
The correct answer choice is (B).
Question 5 :
y - 3x ≤ -10
y + 2x ≥ 45
In the xy-plane, a point with coordinates (h, k) lies in the solution set of the system of inequalities above, what is the minimum possible value of h?
Answer :
The shortcut to solve this kind of questions is to find the point of intersection of the two lines.
The minimum or maximum (not both) value of x will always lie at the point of intersection. Depending on the system of inequalities, the value of x could be minimum or maximum at the point of intersection.
Assume the given inequalities as equations and solve for x.
y - 3x = -10 ----> y = 3x - 10
y + 2x = 45 ----> y = -2x + 45
y = y
3x - 10 = -2x + 45
5x = 55
x = 11
In the point (h, k), h represents x-coordinate, so the minimum possible value of h is 11.
Question 6 :
y ≤ (1/2)x - 5
y ≥ 3x - 20
In the xy-plane, a point with coordinates (h, k) lies in the solution set of the system of inequalities above, what is the maximum possible value of h?
Answer :
As explained the shortcut in the above question, we can solve this problem.
Assume the given inequalities as equations and solve for x.
y ≤ (1/2)x - 5 ----> y = (1/2)x - 5
y ≥ 3x - 20 ----> y = 3x - 20
y = y
(1/2)x - 5 = 3x - 20
Multiply both sides by 2.
x - 10 = 6x - 40
-5x = -30
x = 6
In the point (h, k), h represents x-coordinate, so the maximum possible value of h is 6.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
