SIMPLE INTEREST AND COMPOUND INTEREST

Simple Interest

The formulas given below will be useful to solve problems on simple interest.

I = Prt

A = I + P

A ----> Accumulated value (final value)

P ----> Principal (initial value of an investment)

r ----> Annual interest rate (in decimal)

I ----> Amount of interest

t ----> Time (in years)

Compound Interest

The formulas given below will be useful to solve problems on compound interest.

A = P(1 + r/n)^nt

C.I = A - P

A ----> Accumulated value (final value)

P ----> Principal (initial value of an investment)

r ----> Annual interest rate (in decimal)

n ----> Number of times interest compounded per year

t ----> Time (in years)

C.I ----> Amount of interest

Difference Between Simple Interest and Compound Interest

Important Note :

When we look at the above picture, it is clear that interest earned in S.I and C.I is same ($100) for the 1st year when interest is compounded annually in C.I.

Difference Between Compound and Simple Interest for 2 Years and 3 Years

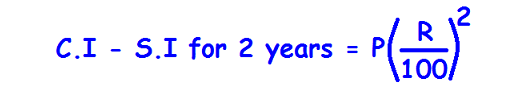
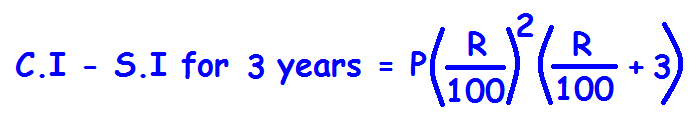
The above two formulas are applicable only in the following conditions.

1. The principal in simple interest and compound interest must be same.

2. Rate of interest must be same in simple interest and compound interest.

3. In compound interest, interest has to be compounded annually.

Solved Examples

Example 1 :

Kyle bought a $2000 government bond that yields 6% in simple interest each year. Write the equation that gives the total amount A, in dollars, Kyle will receive when he sells the bond after t years.

Solution :

Formula for simple interest is

I = Ptr

Substitute.

I = 2000 ⋅ t ⋅ 0.06

= 120t

Final value of the investment :

A = P + I

Substitute 2000 for P and 120t for I.

A = 2000 + 120t

Example 2 :

An investor decides to offer a business owner a $20,000 loan at simple interest of 5% per year. Find the total amount in dollars, the investor will receive when the loan is repaid after 5 years.

Solution :

Formula for simple interest is

I = Ptr

Substitute.

I = 20000 ⋅ 5 ⋅ 0.05

= 5000

Final value of the investment :

A = P + I

= 20000 + 5000

= 25000

So, the investor will receive $25,000 when the loan is repaid after 5 years.

Example 3 :

Jonas has a savings account that earns 3 percent interest compounded annually. If his initial deposit is $1000, find the value of the deposit after 10 years.

Solution :

Formula for final value in compound interest :

A = P(1 + r/n)^nt

Because it is compounded annually,  number of times interest compounded per year is 1. So, n = 1.

Substitute 1000 for P, 0.03 for r, 1 for n and 10 for t.

A = 1000(1 + 0.03/1)^{1 ⋅ 10}

Simplify.

A = 1000(1.03)¹⁰

Use calculator.

A ≈ 1344

So, the value of the deposit after 10 years is about $1,344.

Example 4 :

Jay puts an initial deposit of $400 into a bank account that earns 5 percent interest each year, compounded semiannually. Find the value of the deposit after 4 years.

Solution :

Formula for final value in compound interest :

A = P(1 + r/n)^nt

Because it is compounded semiannually,  number of times interest compounded per year is 2. So, n = 2.

Substitute 400 for P, 0.05 for r, 2 for n and 4 for t.

A = 400(1 + 0.05/2)^{2 ⋅ 4}

Simplify.

A = 400(1 + 0.025)⁸

A = 400(1.025)⁸

Use calculator.

A ≈ 487.4

So, the value of the deposit after 4 years is about $487.40.

Example 5 :

Veronica has a bank account that earns m% interest compounded annually. If she has opened the account with $200 and the expression $200(x)^t represents the amount in the account after t years, then find the value of x in terms of m.

Solution :

Amount in the account after t years (given) :

A = 200(x)^t ----(1)

Formula for final value in compound interest :

A = P(1 + r/n)^nt

Because it is compounded annually, number of times interest compounded per year is 1. So, n = 1.

Rate of interest is m%, so we have

r = m/100

r = 0.01m

Substitute 200 for P, 0.01m for r and 1 for n.

A = 200(1 + 0.01m/1)^{1 ⋅ t}

A = 200(1 + 0.01m)^t ----(2)

Both the expressions (1) and (2) represent the the amount in the account after t years.

Comparing (1) and (2), we get

x = 1 + 0.01m

Example 6 :

Daniel has $1000 in as checking account and $3000 in a savings account. The checking account earns him 1 percent interest compounded annually. The savings account earns him 6 percent interest compounded annually. Assuming he leaves both these accounts alone, write the expression that represents how much more interest Daniel will have earned from the savings account than from the checking account after 5 years.

Solution :

Interest earned in checking account :

C.I = A - P

C.I = P(1 + r/n)^nt - P

C.I = P[(1 + r/n)^nt - 1]

Substitute.

C.I = 1000[(1 + 0.01/1)^{1 ⋅ 5} - 1]

C.I = 1000[(1.01)⁵ - 1]

C.I = 1000(1.01)⁵ - 1000

Interest earned in savings account :

C.I = A - P

C.I = P(1 + r/n)^nt - P

C.I = P[(1 + r/n)^nt - 1]

Substitute.

C.I = 3000[(1 + 0.06/1)^{1 ⋅ 5} - 1]

C.I = 3000[(1.06)⁵ - 1]

C.I = 3000(1.06)⁵ - 3000

The interest earned more in savings account than checking account :

= Interest in savings A/c  -  Interest in checking A/c

= [3000(1.06)⁵ - 3000]  -  [1000(1.01)⁵ - 1000]

= 3000(1.06)⁵ - 3000  -  1000(1.01)⁵ + 1000

= 3000(1.06)⁵ - 1000(1.01)⁵ - 2000

Example 7 :

Kristen opens a bank account that earns 4% interest each year, compounded once every two years. If she had opened the account with k dollars, write the expression that represents the total amount in the account after t years.

Solution :

Formula for final value in compound interest :

A = P(1 + r/n)^nt

Because it is compounded once in two years, we have

n = 1/2 or 0.5

Substitute k for p, 0.04 for r and 0.5 for n.

A = k(1 + 0.04/0.5)^{(0.5) ⋅ t}

Use calculator and simplify.

A = k(1 + 0.08)^{(1/2) ⋅ t}

A = k(1.08)^t/2

Example 8 :

In simple interest, a sum of money doubles itself in 10 years. Find the number of years it will take to triple itself.

Solution :

Let P be the sum of money invested.

P becomes doubles itself in 10 years.

So, P will be 2P in 10 years.

Now we can calculate interest for ten years as shown below.

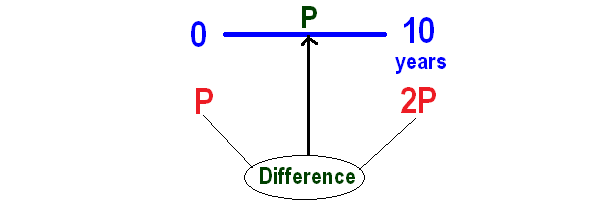
From the above calculation, P is the interest for the first 10 years.

In simple interest, interest earned every year will be same.

So, interest earned in the next 10 years also will be P.

That is,

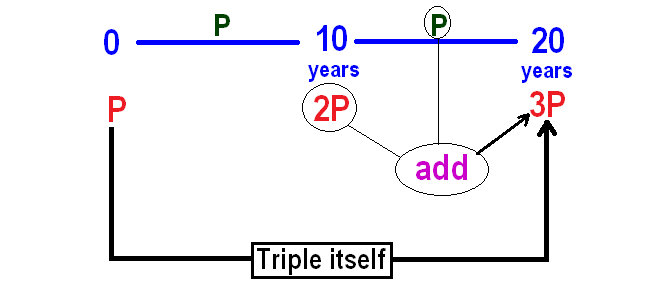
So, it will take 20 years for the principal to become triple itself.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.