SIMPLIFYING SQUARE ROOTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The following steps will be useful to simplify any square root.
(i) Decompose the number inside the square root into prime factors.
(ii) Inside the square root, if the same number is repeated twice with multiplication, it can be taken out of the square root.
(iii) Combine the like square root terms using mathematical operations.
Example :
√27 + √3 - √12 = √(3 ⋅ 3 ⋅ 3) + √3 - √(2 ⋅ 2 ⋅ 3)
= 3√3 + √3 - 2√3
= 2√3
Solved Questions
Simplify each the following square root expressions :
Question 1 :
√64 + √196
Answer :
Because 64 and 196 are perfect squares, we can find the square root of 64 and 194 as shown below.
|
√64 = √(8 ⋅ 8) √64 = 8 |
√196 = √(14 ⋅ 14) √196 = 14 |
√64 + √196 = 8 + 14
= 22
Question 2 :
√40 + √160
Answer :
Decompose 40 and 160 into prime factors using synthetic division.
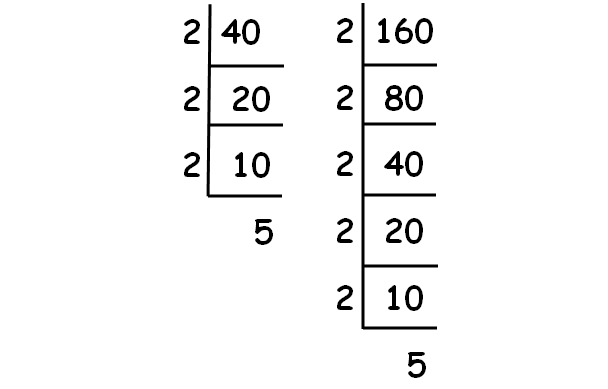
√40 = √(2 ⋅ 2 ⋅ 2 ⋅ 5) = 2√10
√160 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5) = 4√10
√40 + √160 :
= 2√10 + 4√10
= 6√10
Question 3 :
2√425 - 3√68
Answer :
Decompose 425 and 68 into prime factors using synthetic division.
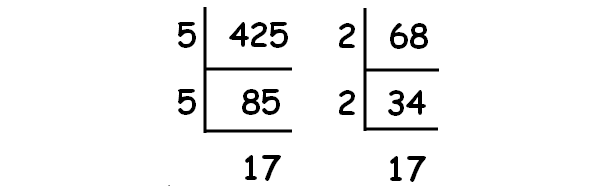
|
√425 = √(5 ⋅ 5 ⋅ 17) √425 = 5√17 |
√68 = √(2 ⋅ 2 ⋅ 17) √68 = 2√17 |
2√425 - 3√68 :
= 2(5√17) - 3(2√17)
= 10√17 - 6√17
= 4√17
Question 4 :
√243 - 5√12 + √27
Answer :
Decompose 243, 12 and 27 into prime factors using synthetic division.
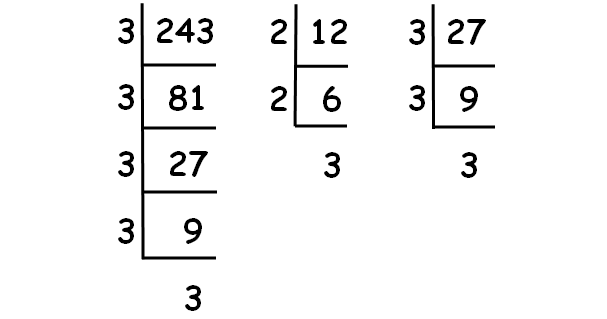
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
√12 = √(2 ⋅ 2 ⋅ 3) = 2√3
√27 = √(3 ⋅ 3 ⋅ 3) = 3√3
√243 - 5√12 + √27 :
= 9√3 - 5(2√3) + 3√3
= 9√3 - 10√3 + 3√3
= 2√3
Question 5 :
-√117 - √52
Answer :
Decompose 117 and 52 into prime factors using synthetic division.
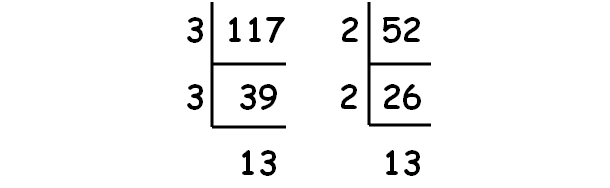
√117 = √(3 ⋅ 3 ⋅ 13) = 3√13
√52 = √(2 ⋅ 2 ⋅ 13) = 2√13
-√117 - √52 :
= -3√13 - 2√13
= -5√13
Question 6 :
(√17)(√51)
Answer :
Decompose 17 and 51 into prime factors.
Because 17 is a prime number, it can't be decomposed anymore. So, √17 has to be kept as it is.
√51 = √(3 ⋅ 17) = √3 ⋅ √17
(√17)(√51) :
= (√17)(√3 ⋅ √17)
= (√17 ⋅ √17)√3
= 17√3
Question 7 :
(√35)(2√15)
Answer :
(√35)(2√15)
Decompose 35 and 15 into prime factors.
√35 = √(5 ⋅ 7) = √5 ⋅ √7
√15 = √(5 ⋅ 3) = √5 ⋅ √3
(√35)(2√15) :
= (√5 ⋅ √7) ⋅ 2(√5 ⋅ √3)
= 2(√5 ⋅ √5)(√7 ⋅ √3)
= 2(5)(√(7 ⋅ 3)
= 10√21
Question 8 :
(14√117) ÷ (7√52)
Answer :
Decompose 117 and 52 into prime factors using synthetic division.
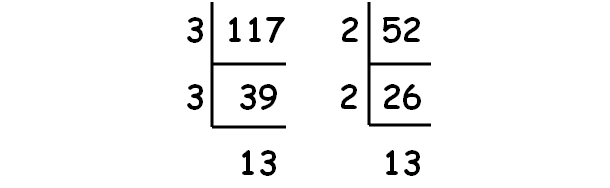
|
√117 = √(3 ⋅ 3 ⋅ 13) √117 = 3√13 |
√52 = √(2 ⋅ 2 ⋅ 13) √52 = 2√13 |
(14√117) ÷ (7√52) :
= 14(3√13) ÷ 7(2√13)
= 42√13 ÷ 14√13
= 42√13/14√13
= 3
Question 9 :
(7√5)2
Answer :
(7√5)2 = 7√5 ⋅ 7√5
= (7 ⋅ 7)(√5 ⋅ √5)
= (49)(5)
= 245
Question 10 :
(√3)3 + √27
Answer :
(√3)3 + √27 = (√3 ⋅ √3 ⋅ √3) + √(3 ⋅ 3 ⋅ 3)
= (3 ⋅ √3) + 3√3
= 3√3 + 3√3
= 6√3
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
