SAT MATH QUESTIONS ON TRIGONOMETRY

Question 1 :

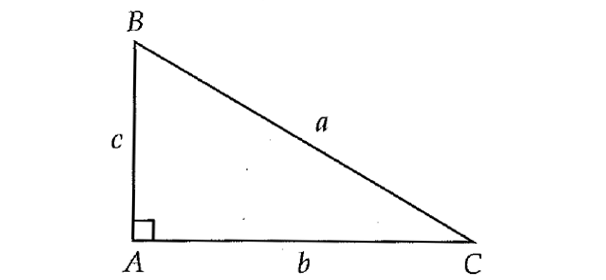
Given right triangle ABC above, which of the following is equal to c/b?

A) tanB

B) 1/tanB

C) cosB

D) 1/cosB

Answer :

In all the given answer choices, we have the angle measure B. Considering the interior angle of B in the right triangle ABC above, AC is the opposite side and AB is adjacent side.

Length of the opposite side = AC = b

Length of the adjacent side = AB = c

The ratio between opposite side and adjacent side is "tan".

b/c = tanB

Take reciprocal on both sides.

c/b = 1/tanB

The correct answer choice is (B).

Question 2 :

sinx = cosy

In the equation above, x and y are measured in radians. Which of the following could be x in terms of y?

A) π/2 - y

B) π/2 + y

C) y - π/2

D) π - y

Answer :

Since sinx and cosx are equal, the angles measures x and y are complementary.

x + y = 90° or π/2

x + y = π/2

x = π/2 - y

The correct answer choice is (A).

Question 3 :

What is the value of sin30° - cos60°?

A) 0

B) (1 - √3)/2

C) (√2 - 1)/2

D) (√3 - 1)/2

Answer :

From the trigonometric ratio table, we have

sin30° = 1/2

cos60° = 1/2

 sin30° - cos60° = 1/2 - 1/2

= 0

The correct answer choice is (A).

Question 4 :

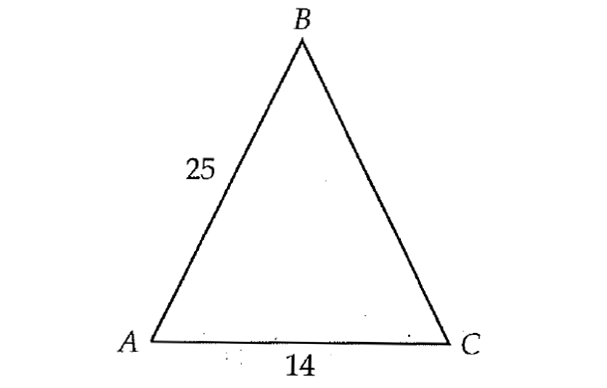
In the triangle above, AB = BC, what is the value of sinA?

A) 0.28

B) 0.56

C) 0.84

D) 0.96

Answer :

In an isosceles triangle, perpendicular drawn to the unequal side will bisect it.

In the triangle ABC above, since AB = AC, it is an isosceles triangle. So, the perpendicular drawn to the unequal side AC will bisect it.

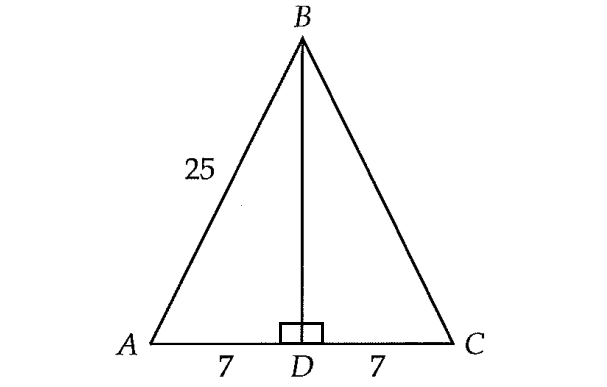
In the right ΔABD, using Pythagorean Theorem,

AD² + BD² = AB²

7² + BD² = 25²

49 + BD² = 625

BD² = 576

BD² = 24²

BD = 24

In the right ΔABD,

sinA = opposite side/ hypotenuse

= BD/AB

= 24/25

= 0.96

The correct answer choice is (D).

Question 5 :

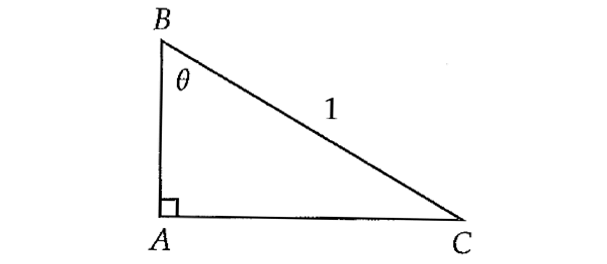
Given right triangle ABC above, which of the following gives the length of AB in terms of θ?

A) sinθ

B) cosθ

C) tanθ

D) 1/sinθ

Answer :

In the right ΔABC above, considering angle θ at the vertex B,

opposite side = AC

adjacent side = AB

hypotenuse = BC

The length of the hypotenuse is given, that is BC = 1 and we have to find the length of the adjacent side.

The ratio between adjacent side and hypotenuse is "cos".

AB/BC = cosθ

AB/1 = cosθ

AB = cosθ

The correct answer choice is (B).

Question 6 :

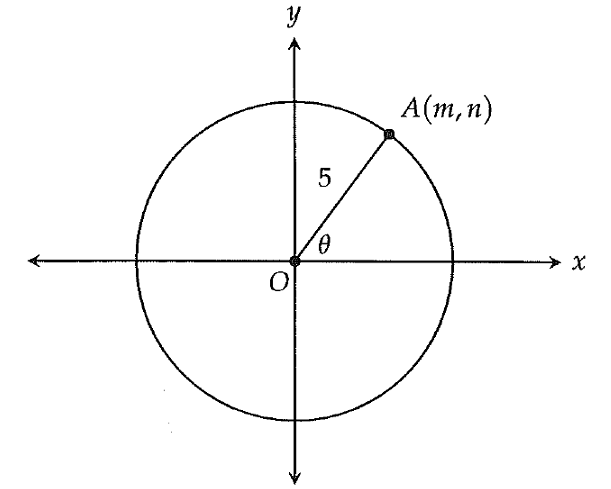
In the xy-plane above, a circle with radius 5 has its center at the origin. Point A lies on the circle and has coordinates (m, n). What is n in terms θ?

A) 5sinθ

B) 5cosθ

C) tanθ

D) 5(sinθ + cosθ)

Answer :

In the given figure, draw a perpendicular from point A to x-axis. Let the perpendicular meet x-axis at B.

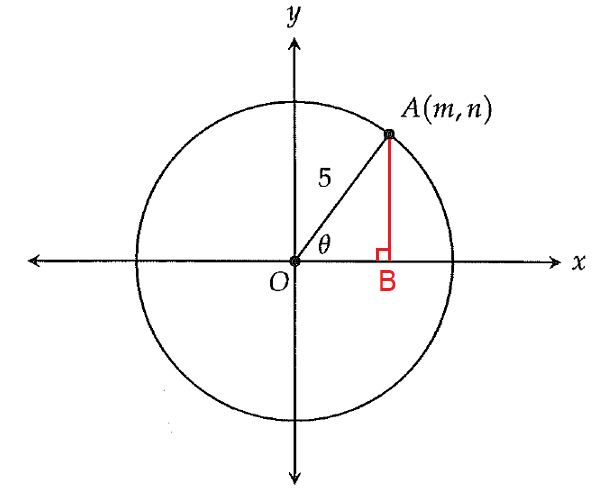
Considering θ in the right ΔOAB in the figure above,

opposite side = AB = n

adjacent side = OB = m

hypotenuse = OA = 5

The length of the hypotenuse is given, that is OA = 5 and we have to find the length of the opposite side AB, that is n.

The ratio between opposite side and hypotenuse is "sin".

AB/OA = sinθ

n/5 = sinθ

n = 5sinθ

The correct answer choice is (A).

Question 7 :

Right triangle ABC is shown in the xy-plane above. What is the value of tanA?

A) 7/12

B) 3/4 

C) 7/9

D) 12/7

Answer :

In the right ΔABC above, considering the angle A,

opposite side = BC

adjacent side = AC

Length of the opposite side :

= BC

= y-coordinate at C - y-coordinate at B

= 4 - (-3)

= 7

Length of the adjacent side :

= AC

= x-coordinate at C - x-coordinate at B

= 7 - (-5)

= 7 + 5

= 12

tanA = opposite side/adjacent side

= BC/AC

= 7/12

The correct answer choice is (A).

Question 8 :

sin24° = cos(3k + 6)°

In the equation above, the angle measures are in degrees. If 0° < k < 90°, what is the value of k?

Answer :

Since sin24° and cos(3k + 6)° are equal, then the angles measures 24° and (3k + 6)° are complementary.

24° + (3k + 6)° = 90°

24 + 3k + 6 = 90

3k + 30 = 90

3k = 60

k = 20

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.