EXPONENTIAL GROWTH AND DECAY

Exponential growth/decay is a specific way that a quantity may increase/decrease over time. 

To solve problems on exponential growth and decay, we have to be aware of exponential growth and decay functions.

Let us consider the following two examples.

When we invest some money in a bank, it grows year by year, because of the interest paid by the bank. 

We buy a car and use it for some years. When it becomes too old, we would like to sell it. 

In the first example, we will be keen to know the final value (Amount invested + Interest) of our deposit. To know the final value of  the deposit, we have to use growth function. 

In the second example, we will be eager to know the sale value of the car (Purchased price - depreciation). Here we have to use decay function. 

In this way, growth and decay functions are being used in our life. 

Exponential Growth

Consider the relationship represented by the table shown below.

In the table above, a constant change of +1 in x corresponds to an increase in y by a constant factor of 4.

Therefore, the relationship given in the table above represents exponential growth, because each y-value is 4 times the value before it.

The points from this table lie on a smooth curve.

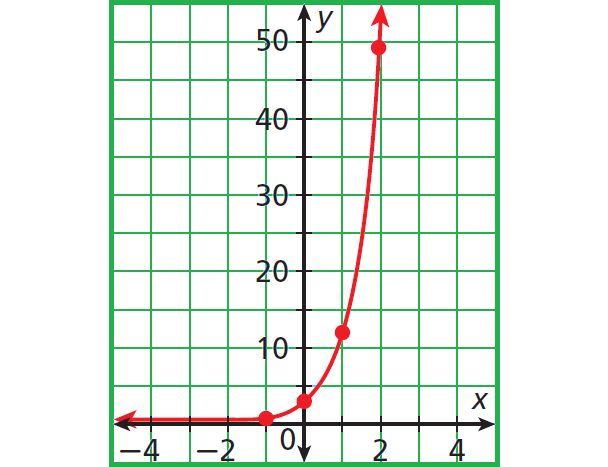
Exponential Decay

Consider the relationship represented by the table shown below.

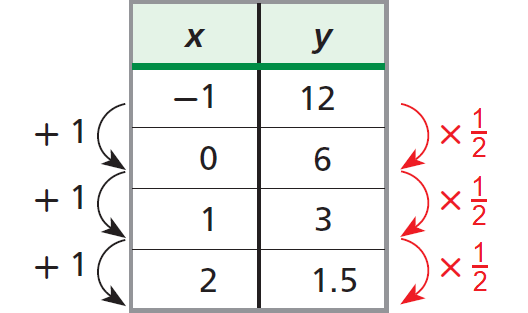
In the table above, a constant change of +1 in x corresponds to a decrease in y by a constant factor of 1/2.

Therefore, the relationship given in the table above represents exponential decay, because each y-value is 1/2 times the value before it.

Formulas

Many real world phenomena are being modeled by functions which describe how things grow or decay as time passes. 

Let us see the formulas which use to estimate and growth and decay. 

Formula 1 :

The formula given below is related to compound interest formula and represents the case where interest is being compounded continuously.  

That is, at any instant the balance is changing at a rate that equals "r" times the current balance.

We use this formula, when it is given "exponential growth/or decay". 

A = Pe^rt

A ---> Ending amount

P ---> Beginning amount

r ---> Growth/Decay rate

t ---> Time

Note :

If it is decay function, the value of r will be negative.

Formula 2 :

The formula given below is compound interest formula and represents the case where interest is being compounded annually or the growth is being compounded once the term is completed. 

A = P(1 + r)ⁿ

A ---> Ending amount

P ---> Beginning amount

r ---> Growth/Decay rate

n ---> No. of years / Time

If it is growth function, we will have r > 0.

If it is decay function, we will have r < 0.

Note :

If it is decay function, the value of r will be negative.

Formula 3 :

The formula given below is related to geometric progression. Here, the initial amount will grow/decay at the constant ratio b.

A = ab^x

A ---> Ending amount

a ---> Beginning amount

b ---> Growth/Decay ratio

x ---> No. of years / terms

Note :

If it is growth function, we will have b > 1.

If it is decay function, we will have 0 < b < 1.

Solved Problems

Problem 1 :

Mark invests $1,500 at a rate of 6% interest compounded annually. How much is the investment worth after 5 years ?

Solution :

Compound Interest Formula :

A = P(1 + r)ⁿ

Substitute P = 1500, r = 6% or 0.06 and n = 5.

A = 1500(1 + 0.06)⁵

= 1500(1.06)⁵

Use a calculator. 

= 2,007.34

So, the worth of the investment after 5 years is about $2,007.34

Problem 2 :

The price of a new automobile is $28,000. If the value of the automobile decreases 12% per year, what will be the price of the automobile after 5 years?

Solution :

Exponential Decay Formula :

A = P(1 - r)ⁿ

Substitute P = 28000, r = 12% or 0.12 and n = 5.

A = 2800(1 - 0.12)⁵

= 1500(0.88)⁵

Use a calculator. 

= 14,776.49

So, the price of the automobile will be about $14,776.49

Problem 3 :

An investment worth $2500 made in a bank which pays 10% interest per year compounded continuously. What will be the value of the investment after 10 years ?

Solution :

We have to use the formula given below to know the value of the investment after 3 years. 

A = Pe^rt

Substitute P = 2500, r = 10% or 0.1, t = 10 and e = 2.71828

A = 2500(2.71828)^(0.1)10

= 6795.70

So, the value of the investment after 10 years is $6795.70.

Problem 4 :

The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture initially, how many bacteria will be present at the end of 8th hour?

Solution :

Note that the number of bacteria present in the culture doubles at the end of successive hours.

Since it grows at the constant ratio "2", the growth is based is on geometric progression. 

We have to use the formula given below to find the no. of bacteria present at the end of 8th hour. 

A = ab^x

Substitute a = 30, b = 2 and x = 8.

A = 30(2⁸)

= 30(256)

= 7680

So, the number of bacteria at the end of 8th hour is 7680.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.