SAT MATH QUESTIONS ON  FUNCTIONS

Question 1 :

The volume of a balloon is given by the equations

V = t² - 3t + 3

What is the volume of the balloon after 3 seconds?

Answer :

To find the volume of the balloon after after 3 seconds, substitute t = 3 in the given equation.

V = 3² - 3(3) + 3

= 9 - 9 + 3

= 3

volume of the balloon after 3 seconds is 3 cubic units.

Question 2 :

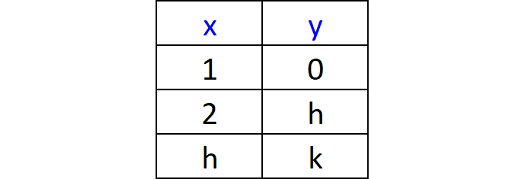
In the table above, if y = x² + x - 2, what is the value of k?

Answer :

From the table, if x = 2, y = h.

Substitute x = 2 and y = h in the given equation.

h = 2² + 2 - 2

h = 4

From the table, if x = h, y = k.

Substitute x = h and y = k in the given equation.

k = h² + h - 2

Substitute h = 4.

k = 4² + 4 - 2

k = 16 + 4 - 2

k = 18

Question 3 :

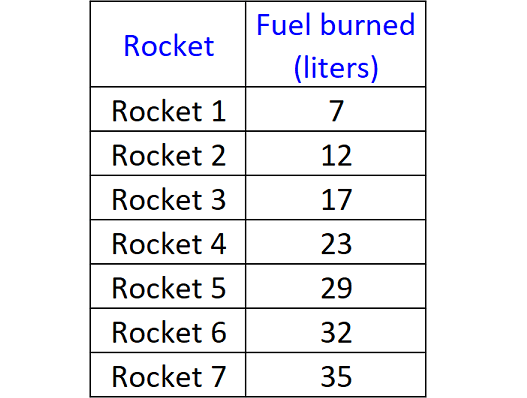
The distance 'd' in meters, traveled by a rocket depends on the amount of fuel 'f' in liters, it burns according to the equation d = (2/3)f. Based on the table above, how many rockets traveled more than 20 meters?

Solution :

d = (2/3)f

Substitute d = 20.

20 = (2/3)f

Multiple both sides by 3/2.

30 = f

When d = 20, f= 30.

That is, if a rocket travels 20 meters of distance, it burns 30 liters of fuel.

So, the rockets burn more than 30 liters of fuel travel more then 20 meters of distance.

In the table above, there are two rockets (rocket 6 and rocket 7) burned more than 30 liters of fuel.

Therefore, there are two rockets traveled more than 20 meters of distance.

Question 4 :

Let the function be f be defined by f(x) = 2x³ - 1 and let the function g be defined by g(x) = x² + 3. Find the value of f[g(1)].

Solution :

g(1) = 1² + 3

= 1 + 3

= 4

f[g(1)] = f(4)

= 2(4)³ - 1

= 2(64) - 1

= 128 - 1

127

Question 5 :

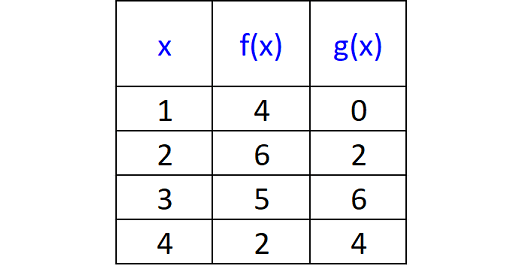
Four values of the functions f and g are shown in the table above. If g(m) = 6, find the value f(m).

Solution :

g(m) = 6 ----(1)

In the table above, when x = 3, g(x) =6.

So,

g(3) = 6 ----(2)

Comparing (1) and (2),

m = 3

f(m) = f(3)

In the table above, when x = 3, f(x) = 5.

Therefore,

f(m) = 5

Question 6 :

An analyst determines that the cost of an order depends on the quantity 'q' ordered in the following way :

C = 3600 - 400q + 20q²

where q ≥ 0. According to this model, for which of the following values of q would the cost of an order be the lowest?

A) 5

B) 10

C) 15

D) 20

Answer :

Substitute the above four values one by one for q in the given cost function.

C(5) = 3600 - 400(5) + 20(5)² = 2100

C(10) = 3600 - 400(10) + 20(10)² = 1600

C(15) = 3600 - 400(15) + 20(15)² = 2100

C(20) = 3600 - 400(20) + 20(20)² = 3600

In the four values of C above, C(10) is the lowest, that is 1600.

When q = 10, the cost of an order would be the lowest.

The correct answer choice is (B).

Question 7 :

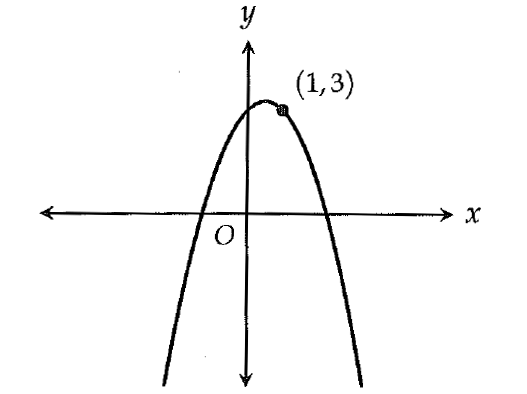
The graph of the function g in the xy-plane is shown above. If f is another function defined in the same xy-plane and f(1) = 1, then g could be which of the following?

A) f - 1

B) f - 2

C) f + 1

D) f + 2

Answer :

Given : f(1) = 1.

So, the point (1, 1) is on the graph of the function f. 

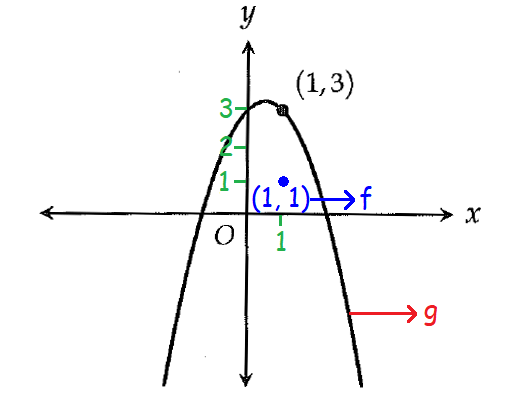
From the picture above, to get the graph of the function g, we have to do a vertical translation of the graph of f by 2 units up.

Thus,

g = f + 2

The correct answer choice is (D) f + 2.

Question 8 :

f(x) = ax³ + b

In the function f defined above, 'a' and 'b' are constants. If f(-1) = 4 and f(1) = 10, find the value of 'b'.

Answer :

f(-1) = 4

a(-1)³ + b = 4

a(-1) + b = 4

-a + b = 4 ----(1)

f(1) = 10

a(1)³ + b = 10

a + b = 10 ----(2)

(1) + (2) :

2b = 14

Divide both sides by 2.

b = 7

Question 9 :

The function f is graphed in the xy-plane shown below.

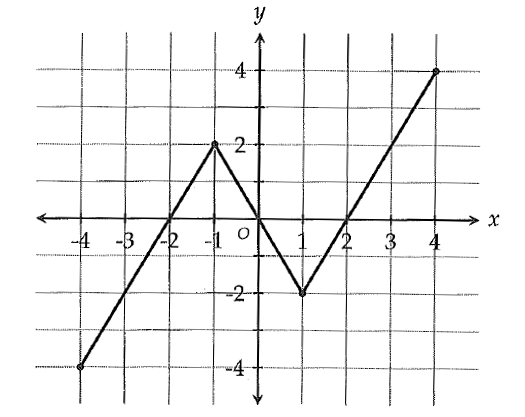
If f(c) = f(3), which of the following could be the value of 'c'?

A) -3

B) -2

C) -1

D) 2

Answer :

In the graph above, when x = 3, f(x) = 2.

That is,

f(3) = 2

It is given that

f(c) = f(3).

Substitute 2 for f(3).

f(c) = 2.

In the graph above, f(x) = 2 when x = -1 or x = 3.

Therefore, c = -1 or 3.

In the given options, we have -1 only.

The correct answer choice is (C) -1.

Question 10 :

For all x ≥ 3, f(x)  = √(x - 3)/2, if f(n) = 3, what is the value of 'n'?

Answer :

f(n) = 3

√(n - 3)/2 = 3

Multiply both sides by 3.

√(n - 3) = 6

Squaring both sides,

n - 3 = 6²

n - 3 = 36

Add 3 to both sides.

n = 39

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.