SAT MATH QUESTIONS ON VOLUME

Question 1 :

The base of a cylinder has a circumference of 5π. The height of the cylinder is 4. What is the volume of the cylinder?

A) 20π

B) 25π

C) 40π

D) 50π

Answer :

Circumference = 5π

2πr = 5π

Divide both sides by 2π.

r = 2.5

Volume of the cylinder :

= πr²h

Substitute r = 2.5 and h = 4.

= π(2.5)²(4)

= π(6.25)(4)

= 25π cubic units

The correct answer choice is (B).

Question 2 :

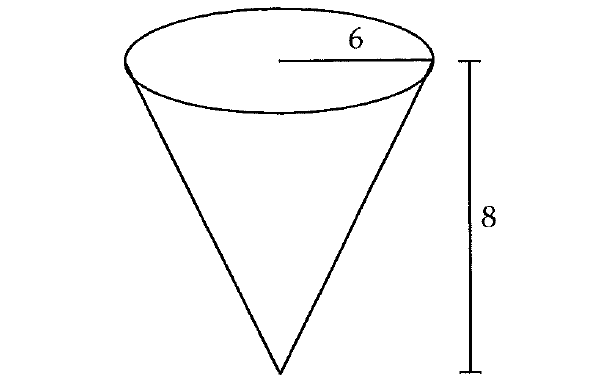
The figure above shows a paper cup in the shape of a right circular cone with a base radius of 6 and a height of 8. The cup is filled with water until its depth reaches half of the height of the cone. What is the volume of the water in the cup?

A) 12π

B) 16π

C) 48π

D) 96π

Answer :

The height of the cone is 8.

When the cup is filled with water until its depth reaches half of the height of the cone, the depth of water in the cone :

= (1/2) x height of the cone

= (1/2) x 8

= 4

Let x be the radius of the water level, when the depth of the water is 4.

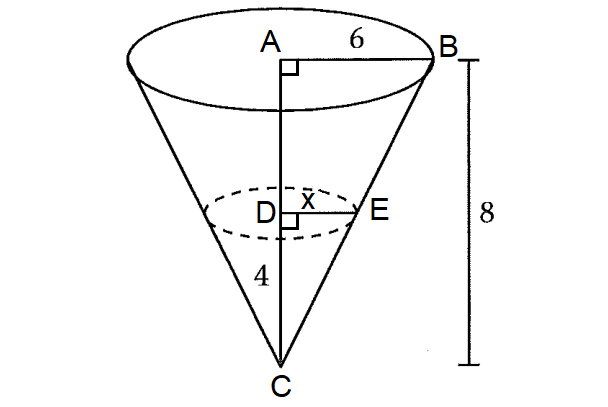
In the figure above, ΔABC and DEC are similar triangles, hence the sides are proportional.

DE/AB = DC/AC

x/6 = 4/8

x/6 = 1/2

x = 3

The radius of the water level is 3.

Since the water is in the cone shaped cup, formula for volume of a cone can be used to find the volume of the water in the cup.

Volume of the water :

= (1/3)πr²h

Substitute r = 3 and h = 4.

= (1/3)π(3)²(4)

= (1/3)π(9)(4)

= 12π cubic units

The correct answer choice is (A).

Question 3 :

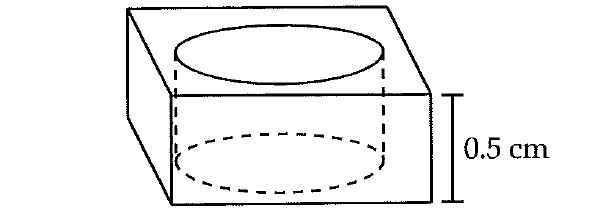
The figure above shows a metal ring with two square faces and a thickness of 0.5 cm. The square faces have a side length of 2.5 cm and the circular hole has a diameter of 2 cm. Which of the following is closest to the volume, in cubic centimeters, of the metal used to form the ring?

A) 1.07

B) 1.55

C) 2.14

D) 3.11

Answer :

Volume of the box with two square faces :

= base area x height

= (2.5 x 2.5) x 0.5

= 6.25 x 0.5

= 3.125 cm³

To find the volume of the ring, we have to subtract the volume of the metal in the hole from the volume of the box. 

The circular hole at the center of the ring is in the shape of the cylinder.

The hole has a diameter of 2 cm. Then the radius of the hole is 1 cm.

Volume of the metal in the hole can be found using the volume of a cylinder formula, as the hole is in the shape of the cylinder. 

Volume of the metal in the hole :

= πr²h

= π(1)²(0.5)

= 0.5π

≈ 1.57 cm³

Volume of the metal ring :

= volume of the box - volume of the metal in the hole

= 3.125 - 1.57

= 1.555 cm³

Of the given answer choices, 1.55 is very close to 1.555.

The correct answer choice is (B).

Question 4 :

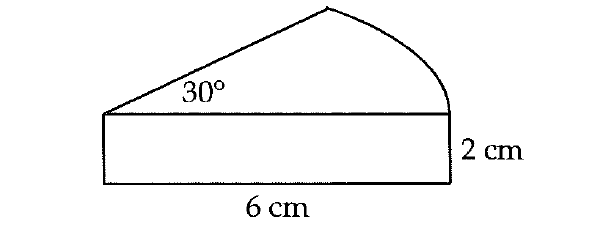
A wedge is formed by a central angle of 30° as shown above was cut from a circular block of cheese with a radius of 6 cm and a thickness of 2 cm. What is the volume, in cubic centimeters, of the wedge?

A) 3π

B) 6π

C) 9π

D) 12π

Answer :

The base of the wedge above is a sector of a circle.

So, area of the base of the wedge can be found using area of a sector of a circle.

Area of the base  of the wedge :

= (θ/360°) x πr²

Substitute θ = 30° and r = 6.

= (30°/360°) x π(6)²

= (1/12) x π(36)

= 3π cm²

Volume of wedge :

= base area x height

= 3π x 2

= 6π cm³

The correct answer choice is (B).

Question 5 :

A rectangular box is 4 in wide, 6 in long, and 8 in deep. If the box is to be filled with cubes, each with a side length of 2 in, until no space is left inside, how many cubes are needed?

A) 12

B) 24

C) 32

D) 48

Answer :

Volume of the box :

= base area x height

= (4 x 6) x 8

= 24 x 8

= 192 in³

Volume of a cube of side length 2 in :

= 2 x 2 x 2

= 8 in³

Number of cubes of side length 2 in are needed to fill the box :

= 192/8

= 24

The correct answer choice is (B).

Question 6 :

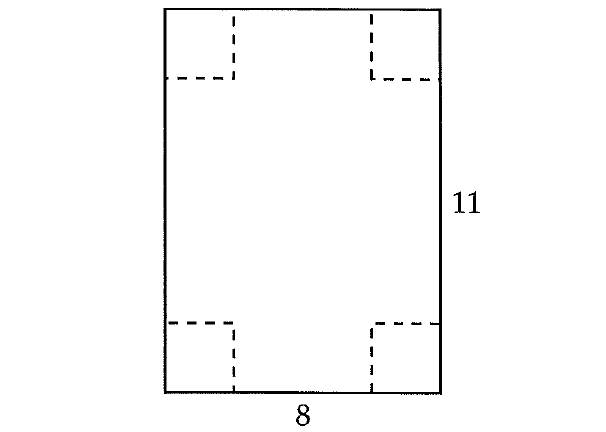
Squares of side length 2 are removed from the corners of an 8 by 11 piece of paper shown above by cutting along the dashed lines. The sides of the paper are then folded up to create a rectangular box with an open top. How many cubes of side length 1 are needed to completely fill the box?

Answer :

After removing squares of side length 2 from the corners, the paper will look like as shown below.

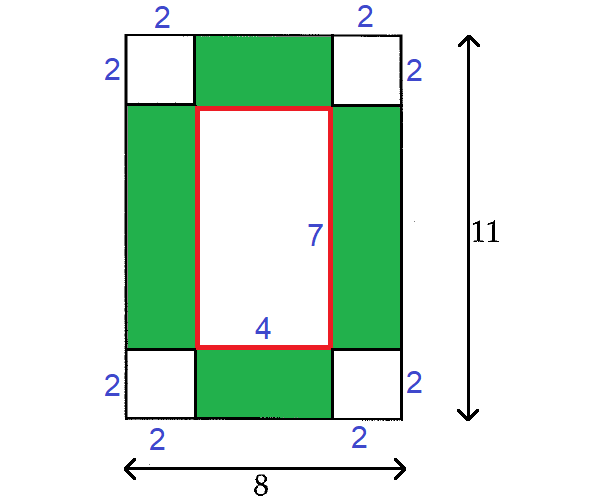
The green colored regions are folded up to create a rectangular box with an open top.

Now, the base of the box is a rectangle with dimensions 4 and 7 and the height of the box is 2.

Volume of the box :

= base area x height

= (4 x 7) x 2

= 28 x 2

= 56 cubic units

Volume of a cube of side length 1 :

= 1 x 1 x 1

= 1 cubic unit

Number of cubes of side length 1 are needed to completely fill the box :

= 56/1

= 56

Question 7 :

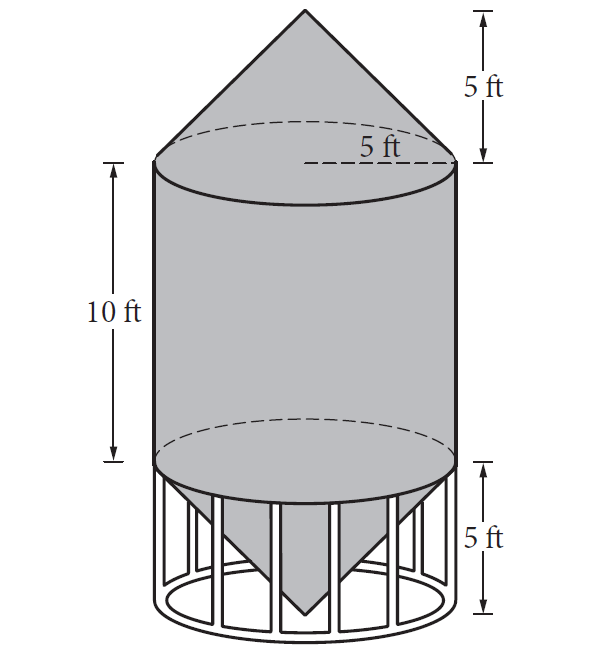
A grain silo is built from two right circular cones and a right circular cylinder with internal measurements represented by the figure above. Of the following, which is closest to the volume of the grain silo, in cubic feet?

A) 261.8

B) 785.4

C) 916.3

D) 1,047.2

Answer :

The volume of the grain silo can be found by adding the volumes of all the solids of which it is composed. The silo is made up of a cylinder with height 10 ft. and base radius 5 feet and two cones, each having height 5 ft. and base radius 5 ft.

Volume of cylinder :

= πr²h

= π(5)²(10)

= 250π

Volume of cone :

= (1/3)πr²h

= (1/3)π(5)²(5)

= (125/3)π

Volume of the grain silo :

= volume of the cylinder + 2 x volume of the cone

= 250π + 2(125/3)π

= 250π + (250/3)π

= 1000π/3

≈ 1047.2 ft³

The correct answer choice is (D).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.