REFLECTING IN THE COORDINATE PLANE

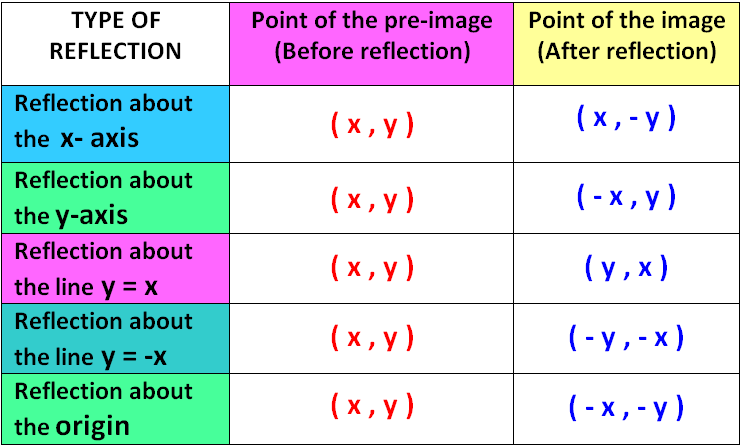
A point on a coordinate plane can be reflected across an axis. The reflection is located on the opposite side of the axis, at the same distance from the axis.

Rules on finding reflected image

Reflection About the X-Axis

Reflection About the Y-Axis

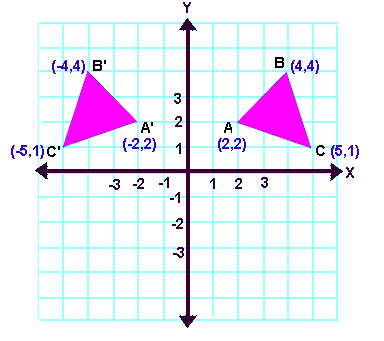
Reflection About the Y = X

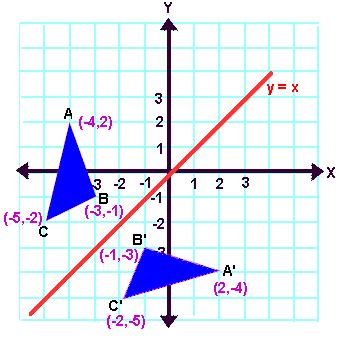
Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection -transformation of a figure.

For example, if we are going to make reflection transformation of the point (2,3) about x-axis, after transformation, the point would be (2,-3). Here the rule we have applied is (x, y) ----> (x, -y). 

So we get (2,3) ----> (2,-3).

Reflection Over Any Line

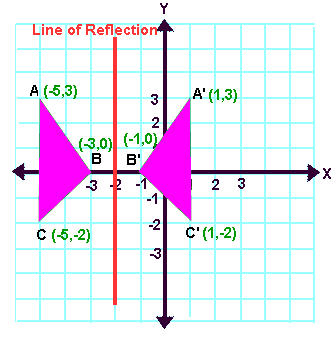
When we look at the above figure, it is very clear that each point of a reflected image A'B'C' is at the same distance from the line of reflection as the corresponding point of the original figure. 

In other words, the line x = -2 (line of reflection) lies directly in the middle between the original figure and its image.

And also, the line x = -2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image. 

Students can keep this idea in mind when they are working with lines of reflections which are neither the x-axis nor the y-axis. 

Problem 1 :

To reflect a point in the x-axis, the x-coordinate remains the same and the y-coordinate is _________

Solution :

To reflect a point in the x-axis, the x-coordinate remains the same and the y-coordinate is negated.

Problem 2 :

 To reflect a point in the y-axis, the y-coordinate remains the same and the x-coordinate is __________

Solution :

 To reflect a point in the y-axis, the y-coordinate remains the same and the x-coordinate is negated.

Problem 3 :

Graph (4,5) on the grid below. Then reflect it in the x-axis. What are the coordinates of the reflection? 

Solution :

(4,-5)

Problem 4 :

 Graph (-2,-4) on the grid below. Then reflect it in the y-axis. What are the coordinates of the reflection?

Solution :

(2,-4)

Problem 5 :

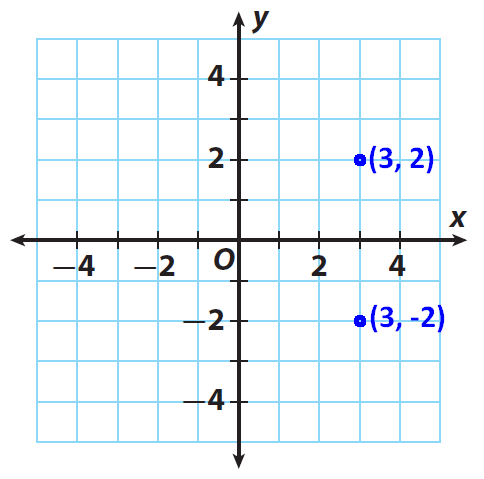
Graph (3, −2). Then fold your coordinate plane along the y-axis and find the reflection of (3, −2). Record the coordinates of the new point in the table.

Solution :

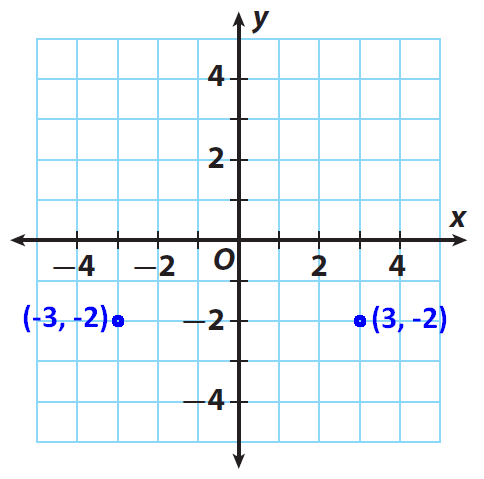
Problem 6 :

Graph (3, −2). Then fold your coordinate plane along the x-axis and find the reflection of (3, −2). Record the coordinates of the new point in the table.

Solution :

Based on the above examples, answer the question given below. 

Problem 7 :

What is the relationship between the coordinates of a point and the coordinates of its reflection across each axis ?

Answer :

Across y-axis :

Opposite x-coordinate and same y-coordinate as the original point.

Across x-axis :

Same x-coordinate and opposite y-coordinate as the original point.

Problem 8 :

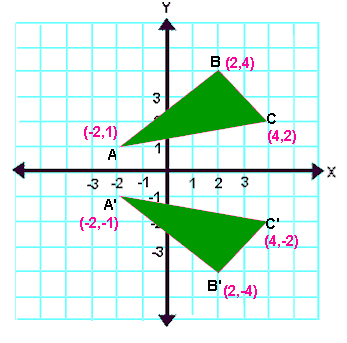
Let A (-2, 1), B (2, 4) and (4, 2) be the three vertices of a triangle. If this triangle is reflected about x-axis, what will be the new vertices A' , B' and C' ?

Solution :

Step 1 :

First we have to know the correct rule that we have to apply in this problem.

Step 2 :

Here triangle is reflected about x - axis. So the rule that we have to apply here is (x , y) -------> (x , -y)

Step 3 :

Based on the rule given in step 1, we have to find the vertices of the reflected triangle A'B'C'

Step 4 :

(x , y) ----> (x , -y)

A(-2, 1) ----> A'(-2, -1)

B(2, 4) ----> B'(2, -4)

C(4, 2) ----> C'(4, -2)

Step 5 :

Vertices of the reflected triangle are

A'(-2, -1), B(2, -4) and C'(4, -2) 

Problem 9 :

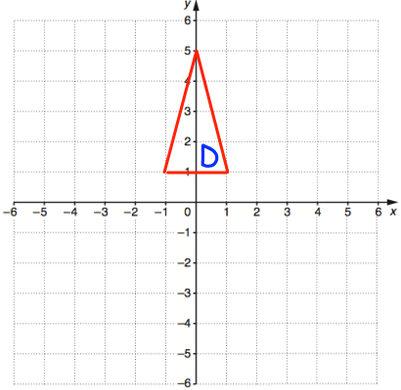
Reflect shape D in the line y = 2

Solution :

Coordinates on the shape D,

(-1, 1) (1, 1) and (0, 5)

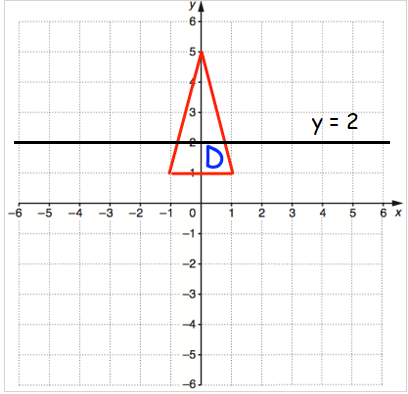
Finding the distance between

• (-1, 1) to line of reflection is 1 unit.
• (1, 1) to the line of reflection is 1 unit.
• (0, 5) to the line of reflection is 3 units.

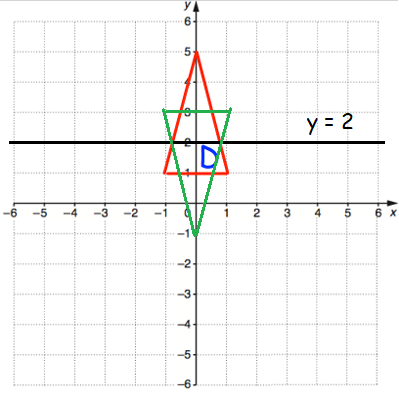
Points of reflection, are

(-1, 3), (1, 3) and (0, -1)

Problem 10 :

Reflect the shape E in the line x = -1

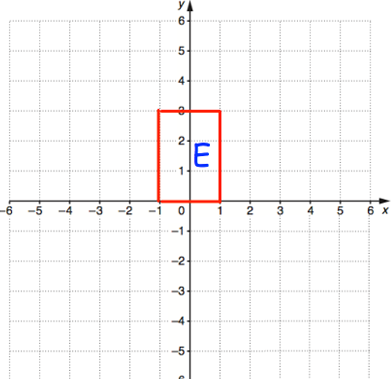
Solution :

The vertices are (-1, 0), (1, 0) (1, 3) and (-1, 3).

By drawing the line of reflection,

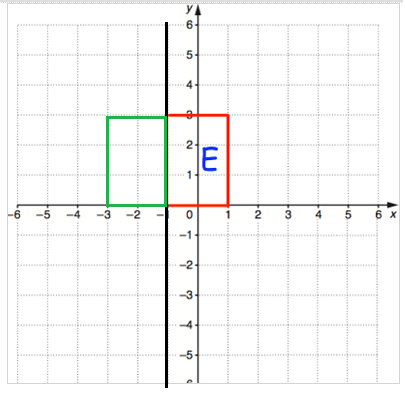
the reflection points are (-1, 0) (-1, 3) and (-3, 0) and (-3, 3).

Problem 11 :

Reflect triangle A in the x-axis.

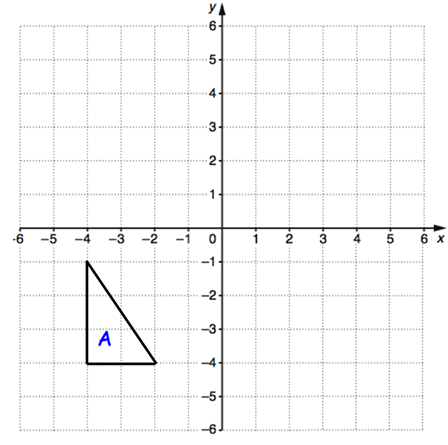
Solution :

Coordinates on the shape A,

(-4, -1) (-4, -4) and (-2, -4)

Point after reflection are,

(-4, 1), (-4, 4) and (-2, 4)

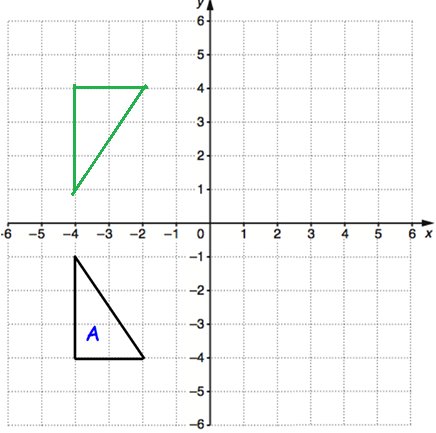
Problem 12 :

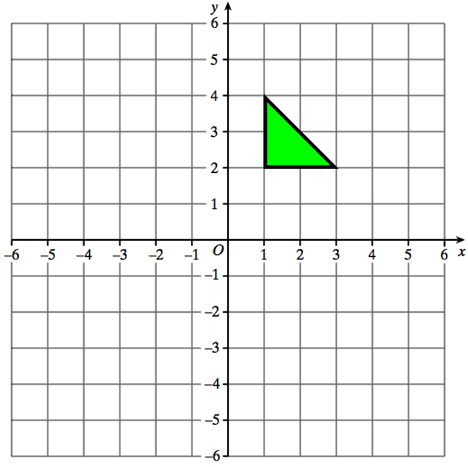
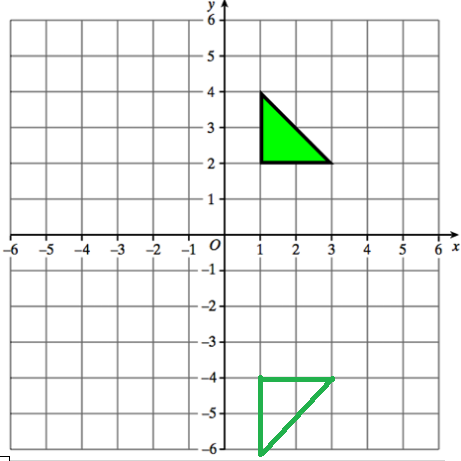
Reflect the triangle in the line y = −1 Label the new triangle B.

Solution :

First draw the line of reflection horizontal line y = -1

The vertices of the original triangle are,

(1, 2) (1, 4) and (3, 2)

Finding the vertical distance between each vertices and line of reflection, we get the new coordinates

(1, -4), (-1, 6) and (3, -4)

Problem 13 :

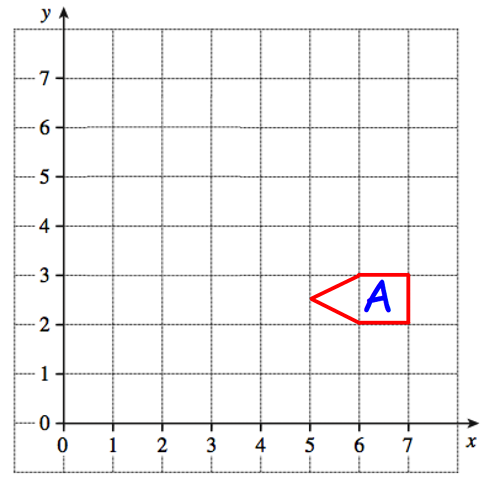
Reflect shape A in the line x = 4 Label the new triangle B.

Solution :

The original coordinates are (6, 2) (7, 2) (7, 3) (6, 3) and (5, 2.5)

Drawing the line of reflection and calculating the horizontal distance between each point, we get

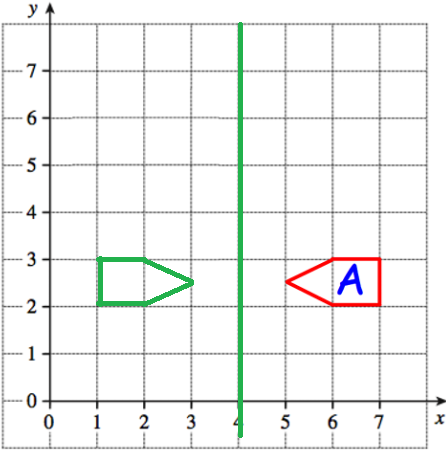
The new coordinates are (3, 2.5) (2, 2) (2, 3) (1, 2) and (1, 3).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.