SAT MATH QUESTIONS ON MEDIAN

Question 1 :

Following are the marks of 7 students in grade 10. Find the median mark.

72, 85, 56, 80, 65, 52, 68

Answer :

To find the median mark, arrange the marks of 7 students from least to greatest.

52, 56, 65, 68, 72, 80, 85

Median = [(n + 1)/2]^th value

Substitute n = 7.

= [(7 + 1)/2]^th value

= (8/2)^th value

= 4^th value

= 80

The median mark is 80.

Question 2 :

Following are the wages of 8 workers expressed in $. Find the median wages.

56, 82, 96, 120, 110, 82, 106, 100

Answer :

To find the median wages, arrange the wages of 8 workers from least to greatest.

56, 82, 82, 96, 100, 106, 110, 120

Median = [(n + 1)/2]^th value

Substitute n = 8.

= [(8 + 1)/2]^th value

= (9/2)^th value

= 4.5^th value

= average of 4^th and 5^th values

= (96 + 100)/2

= 98

The median wages is $98.

Question 3 :

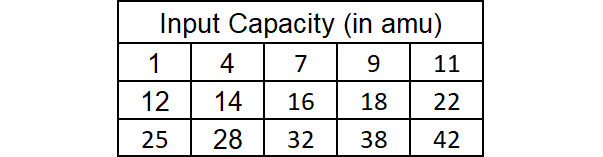
The table above gives the atomic mass, to the nearest amu, of 15 different elements. Based on the table, what is the median atomic mass, in amu, of these elements?

A) 14

B) 15

C) 16

D) 18

Answer :

The atomic mass, to the nearest amu of 15 different elements are already arranged from least to greatest.

Median = [(n + 1)/2]^th value

Substitute n = 15.

= [(15 + 1)/2]^th value

= (16/2)^th value

= 8^th value

= 16

The correct answer choice is (C).

Question 4 :

A sociologist chose 300 students at random from each of two schools and asked each student how many siblings he or she has. The results are shown in the table below.

Students’ Sibling Survey

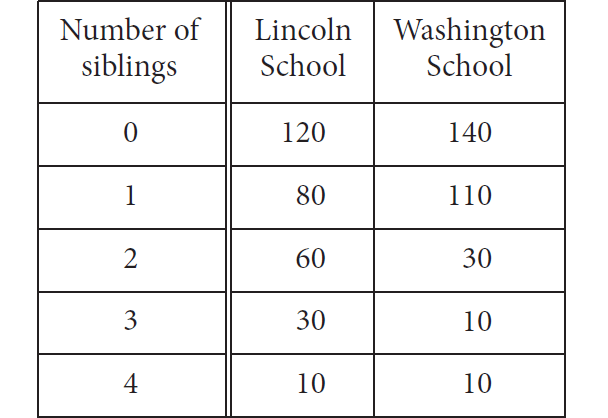
There are a total of 2,400 students at Lincoln School and 3,300 students at Washington School.

What is the median number of siblings for all the students surveyed?

A) 0

B) 1

C) 2

D) 3

Answer :

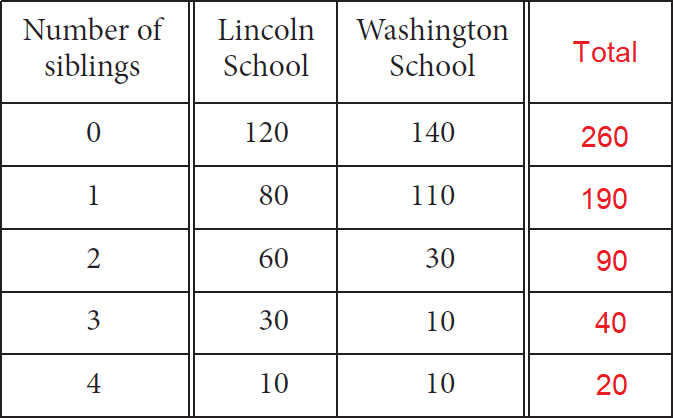
Total number of students surveyed in both Lincoln school and Washington school :

= 260 + 190 + 90 + 40 + 20

= 600

Formula to find median for a data which contain 'n' number of values :

= [(n + 1)/2]^th value

Substitute n = 600.

= [(600 + 1)/2]^th value

= (601/2)^th value

= 300.5^th value

In the table above, in both the 1^st category '0' siblings and the 2^nd category '1' sibling, there are

= 260 + 190

= 450 students

In the 1^st category '0' siblings, there are 260 siblings.

So, it is clear that 300.5^th value comes in the 2^nd category '1' sibling.

Therefore, median number of siblings for all the students surveyed is '1'.

The correct answer choice is (B).

Question 5 :

The table below gives the distribution of weights, to the nearest pound, for 50 lobsters harvested off the coast of Maine and 50 lobsters harvested off the coast of Massachusetts.

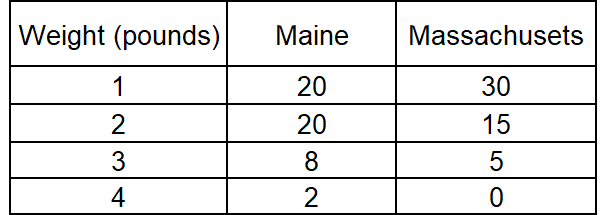
According to the data, which of the following accurately compares the median weight of the lobsters harvested off the coast of Maine with that of the lobsters harvested off the coast of Massachusetts?

A) The median weight of the lobsters from Maine is one pound less than that of the lobsters from Massachusetts.

B) The median weight of the lobsters from Maine is one pound more than that of the lobsters from Massachusetts.

C) The median weight of the lobsters from Maine is half a pound more than that of the lobsters from Massachusetts.

D) The median weight of the lobsters from Maine is the same as that of the lobsters from Massachusetts.

Answer :

Maine :

Total number of lobsters is

= 20 + 20 + 8 + 2

= 50

Median = [(n + 1)/2]^th value

Substitute n = 50.

= [(50 + 1)/2]^th value

= (51/2)^th value

= 25.5^th value

In the table above, for Maine, there are 20 lobsters in the first category 1 pound and 20 lobsters in the second category 2 pounds.

It is clear that 25.5^th value comes in the second category 2 pounds.

So, the median weight of the lobsters from Maine is 2 pounds. 

Massachusetts :

Total number of lobsters is

= 30 + 15 + 5 + 0

= 50

Median = [(n + 1)/2]^th value

Substitute n = 50.

Median = 25.5^th value

In the table above, for Massachusetts, there are 30 lobsters in the first category '1' pound.

It is clear that 25.5^th value comes in the first category itself, which is 1 pound.

So, the median weight of the lobsters from Massachusetts is 1 pounds.

Therefore, the median weight of the lobsters from Maine is one pound more than that of the lobsters from Massachusetts.

The correct answer choice is (B).

Question 6 :

A printer's input capacity is the maximum number of sheets of paper the printer can hold at one time. The table below gives the distribution of input capacities for a randomly selected group of printers.

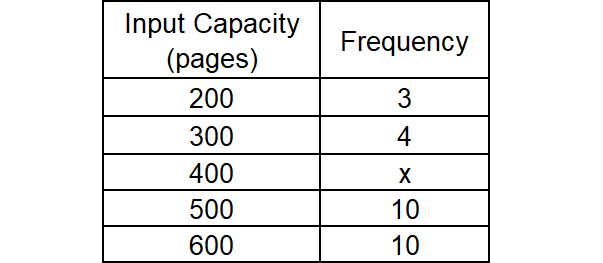
If the median input capacity of these printers is 400 pages, what is the minimum possible value of x?

Answer : 

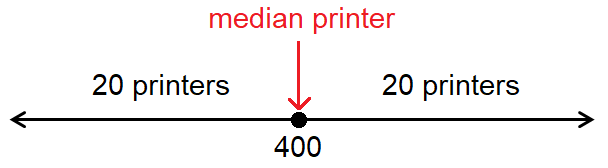
The median is 400.

Since there are already 20 printers on the right side of the median, there must be 20 printers on the left side also. Including 1 printer at the median, we have 41 printers in all. 

From the table above, there are already 7 printers with an input capacity below 400. So, must have 13 more printers equal to 400, plus one more at 400 to  be the median. That's a total of 14 for x.

Therefore the minimum possible value of x is 14.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.