PERCENT CHANGE

Percentage change is all about measuring change from old value to new value per hundred.

For example, the value 1000 is changed to 1200.

Here, the actual change is 200.

But, what is the change per hundred?

The initial value is 1000 and there are ten 100's in it. So, to know the change per hundred, we need to divide the actual change 200 by 10.

200/10 = 20

Therefore, the change per hundred is 20.

So, the percent change from the value 1000 to 1200 is

20%

Percentage Change Formula

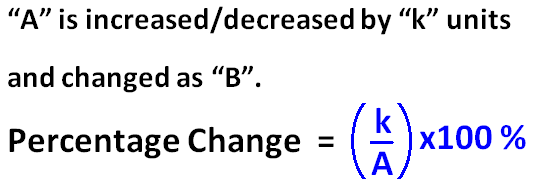
Other Cases

Case (i) :

If a quantity, say A is increased by k%, then the quantity after increase :

= .(100 + k)% of A

= (100 + k)% ⋅ A

Case (ii) :

If a quantity, say A is decreased by k%, then the quantity after decrease :

= (100 - k)% of A

= (100 - k)% ⋅ A

Example 1 :

The price of a product is increased from $25 to $30. Find the percent increase.

Solution :

Find the amount of change.

Amount of change  =  Greater value - Lesser value

=  30 - 25

=  5

Percentage change is

= (Amount of change / Original amount) x 100%

= (5 / 25) ⋅ 100%

= 0.2 ⋅ 100 %

= 20 %

So, the percent increase from $25 to $30 is 20%.

Example 2 :

Find the percent decrease from 90 inches to 63 inches.

Solution :

Find the amount of change.

Amount of change = Greater value - Lesser value

= 90 - 63

= 27

Percentage change is

= (Amount of change/Original amount) x 100%

= (27/90) ⋅ 100%

= 0.3 ⋅ 100 %

= 30 %

So, the percent decrease from 90 inches to 63 inches is 30%.

Example 3 :

The price of a product is $30. If the price is increased by 15%, then find the new price.

Solution :

The new price is

= (100 + 15)% of 30

= 115% ⋅ 30

= (115/100) ⋅ 30

= 1.15 ⋅ 30

= 34.5

So, the new price after 15% increase is $34.50.

Example 4 :

The cost price of a product is $150 and it is sold at a loss of 30%. Find the selling price of the product.

Solution :

Because the product is sold in loss, the cost price has to be decreased by 30% to find the selling price.

The selling price of the product is

= (100 - 30)% of 150

= 70% ⋅ 150

= (70/100) ⋅ 150

= 0.7 ⋅ 150

= 105

So, the selling price of the product is $105.

Example 5 :

John got 50% of the questions correct on a 40-question test and 80% on a 80-question test. What percent of all questions did John get correct?

Solution :

Number of questions he got correct in 40-question test is

= 50% ⋅ 40

= 0.5 ⋅ 40

= 20

Number of questions he got correct in 80-question test is

= 80% ⋅ 80

= 0.8 ⋅ 80

= 64

Number of questions he got correct in both the tests is

= 20 + 64

= 84

Total number of questions in both the tests is

= 40 + 80

= 120

Percent of questions John got correct is

= (84/120) ⋅ 100%

= 70%

So, John got 70% of all questions correct.

Example 6 :

The price of a dress is increased by 20%, then decreased by 40%, then increased by 25%. the final price is what percent of the original price?

Solution :

Let $100 be the original price.

Price after 20% increase :

= (100 + 20)% ⋅ 100

= 120% ⋅ 100

= 1.2 ⋅ 100

= 120

Price after 40% decrease :

= (100 - 40)% ⋅ 120

= 60% ⋅ 120

= 0.6 ⋅ 120

= 72

Price after 25% increase :

= (100 + 25)% ⋅ 72

= 125% ⋅ 72

= 1.25 ⋅ 72

= 90

Original price is $100 and final price is $90.

So, the final price is 90% of the original price.

Example 7 :

If x is 50% larger than z, and y is 20% larger than z, then x is what percent larger than y?

Solution :

Let z = 100.

Finding the value of x :

x = (100 + 50)% ⋅ 100

x = 150% ⋅ 100

x = 1.5 ⋅ 100

x = 150

Finding the value of y :

y = (100 + 20)% ⋅ 100

y = 120% ⋅ 100

y = 1.2 ⋅ 100

y = 120

Difference between the value of x and y is

= 150 - 120

= 30

Percent change :

= (30 / 120) ⋅ 10%

= 25%

So, x is 25% larger than y.

Example 8 :

The number of students at a school decreased 20% from 2015 to 2016. If the number of students enrolled in 2016 was k, find the number of students enrolled in 2015 in terms of k.

Solution :

Number of students enrolled in 2016 = k.

Let x be the number of students enrolled in 2015.

Number of students enrolled in 2016 was decreased by 20% compared to 2015.

So, we have

Number of students enrolled in 2016 = (100 - 20)% ⋅ x

k = 80% ⋅ x

k = (80/100) ⋅ x

k = (4/5) ⋅ x

Multiply each side by 5/4.

(5/4) ⋅ k = x

1.25k = x

So, the number of students enrolled in 2015 is 1.25k.

Example 9 :

Townsend Realty purchased a property for $140,000 after having received a 40% discount off the original price along with an additional 20% off the discounted price for purchasing the property in cash. Find the original price of the property (Round the answer to the nearest dollar).

Solution :

Let x be the original price of the property.

The price of the property after 40% discount :

= (100 - 40)% of x

= 60% ⋅ x

= 0.6x

The price of the property after additional 20% off :

= (100 - 20)% of 0.6x

= 80% ⋅ 0.6x

= 0.8 ⋅ 0.6x

= 0.48x

Therefore, the purchased price is 0.48x.

But, the purchased price given in the question is $140,000.

Then, we can have

0.48x = 140000

Divide each side by 0.32

x ≈ 291,667

So, original price of the property is about $291,667.

Example 10 :

Among 9th graders at a school, 30% of the students are Red Sox fans. Among those Red Sox fans, 40% are also Celtics fans. What percent of the 9th graders at the school are both Red Sox fans and Celtics fans?

Solution :

Let 100 be the strength of 9th graders.

Number of Red Sox fans :

= 30% ⋅ 100

= 0.3 ⋅ 100

= 30

Number of Celtics and Red Sox fans :

= 40% ⋅ 30

= 0.4 ⋅ 30

= 12

Out of 100 students in 9th grade, 12 students are both Red Sox and Celtics fans.

So, 12% of the 9th graders are both Red Sox and Celtics fans.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.