SAT MATH QUESTIONS ON PROPORTIONS

A proportion is an equation stating that two ratios are equal.

The proportions a : b = c : d is read " a is to b as c is to d". The numbers a and d are called the extremes of the proportion. The numbers b and c are called the means of the proportion.

Cross Product Rule :

In a proportion, the product of the extremes is equal to the product of the means. This is called cross product rule.

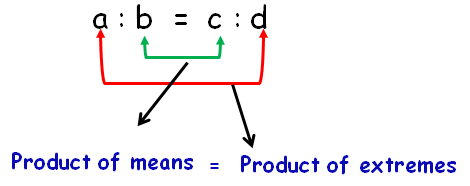
If a/b = c/d, then ad = bc. The products ad and bc are called the cross products of the proportion a/b = c/d.

Example 1 :

Find the value of x :

3/7 = 6/(x - 4)

Solution :

Using cross product rule,

3(x - 4) = 6(7)

3x - 12 = 42

3x = 54

x = 18

Example 2 :

Carter’s SUV requires 8 gallons of gasoline to travel 148 miles. How much gasoline, to the nearest gallon, will he need for a 500 mile trip?

Solution :

Given : 8 gallons of gasoline required to travel 148 miles. 

Let x be the amount of gasoline in gallons required for a 500 mile trip.

Write a proportion :

8 : 148 = x : 500

Using cross product rule,

148x = 8(500)

x ≈ 27

Carter’s needs about 27 gallons of gas for a 500 mile trip.

Example 3 :

The actual distance between two towns is 90 miles. If the scale is 1 inch = 30 miles, what is the distance between the two towns on the map?

Solution : 

Let x be the distance between the two towns on the map in inches.

Write a proportion.

1 : 30 = x : 90

Using cross product rule,

30x = 90

x = 3

So, the distance between the towns on the map is 3 inches.

Example 4 :

The ratio between the number of boys and girls in a school is 3 : 5. If there are 270 boys, find the number of girls in the school.

Solution :

Let x be the number of boys in the school.

Write a proportion.

3 : 5 = 270 : x

Using cross product rule,

3x = 5(270)

3x = 1350

x = 450

There are 450 girls in the school.

Example 5 :

On a map, 1 inch represents 5 miles. If a certain state is represented on a map by a rectangle 10 inches by 7.2 inches, what is the area of the state in square miles?

A) 360 mi²

B) 720 mi²

C) 1080 mi²

D) 1800 mi²

Solution :

Let 10 inches represents x miles.

Write a proportion.

1 : 5 = 10 : x

Using cross product rule,

x = 50 miles

Let 7.2 inches represents y miles.

Write a proportion.

1 : 5 = 7.2 : y

Using cross product rule,

y = 36 miles

The area of the state :

= length ⋅ width

= 50 ⋅ 36

= 1800 mi²

The correct answer choice is (D).

Example 6 :

If the kinetic energy of a moving tennis ball is doubled, its velocity must have increased by what factor?

A) 4

B) 2

C) √3

D) √2

Solution :

Formula for kinetic energy.

K.E = (1/2)mv²

When the kinetic energy is doubled, let us assume that the velocity has to be increased by the factor 'x'.

Write a proportion.

K.E : (1/2)mv² = 2(K.E) : (1/2)m(xv)²

K.E : 0.5mv² = 2(K.E) : 0.5mx²v²

Using cross product rule,

K.E(0.5mx²v²) = 2(K.E)(0.5mv²)

x² = 2

x = √2

If the kinetic energy of a moving tennis ball is doubled, its velocity must have increased by the factor √2.

The correct answer choice is (D).

Example 7 :

A radioactive element loses 15 percent of its mass and 20 percent of its velocity. By what percent has its kinetic energy decreased?

A) 32%

B) 36.2%

C) 54.4%

D) 45.6%

Solution :

After 15% loss in mass and 20% in velocity, let the kinetic energy be y% of its original amount.

Write a proportion.

K.E : (1/2)mv²  =  (y/100)K.E : (1/2)(0.85m)(0.8v)²

K.E : 0.5mv²  =  0.01yK.E : 0.272mv²

Using cross product rule,

K.E(0.272mv²) = 0.01yK.E(0.5mv²)

0.272 = 0.01y(0.5)

0.272 = 0.005y

54.4 = y

100% - 54.4% = 45.6%

After the radioactive element loses 15 percent of its mass and 20 percent of its velocity, the kinetic energy has decreased by 45.6%.

The correct answer choice is (D).

Example 8 :

A cylinder has a base radius of r and a height of h. If the radius is reduced by 30%, how would the volume of the cylinder change?

A) The volume would be decreased by 49 percent.

B) The volume would be decreased by 50 percent.

C) The volume would be decreased by 51 percent.

D) The volume would be decreased by 60 percent.

Solution :

Formula for volume of a cylinder :

V = πr²h

After the radius is reduced by 30%, let the volume of the cylinder be y% of its original value.

Write a proportion.

V : πr²h  =  (y/100)V : π(0.7r)²h

V : πr²h = 0.01yV : 0.49πr²h

Using cross product rule,

V(0.49πr²h) = 0.01yV(πr²h)

0.49 = 0.01y

49 = y

100% - 49% = 51%

If the radius is reduced by 30%, the volume of the cylinder would be decreased by 51%.

The correct answer choice is (C).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.