ANALYTICAL GEOMETRY FORMULAS

Distance between two points :

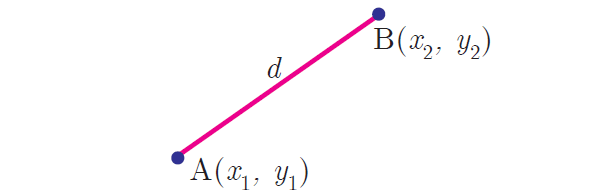
Distance between two points A(x₁, y₁) and B(x₂, y₂) is

Mid-point of line segment :

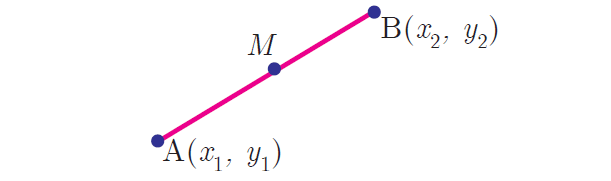
The mid-point M, of the line segment joining A(x₁, y₁) and B(x₂, y₂) is

Section Formula (Internal Division) :

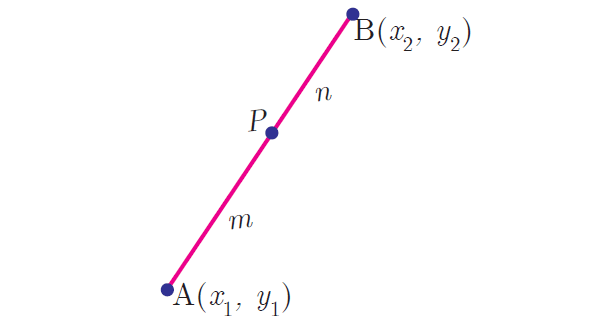
Let A(x₁, y₁) and B(x₂, y₂) be two distinct points such that point p(x, y) divides AB internally in the ratio m : n.

Then the coordinates of P are given by

Section Formula (Internal Division) :

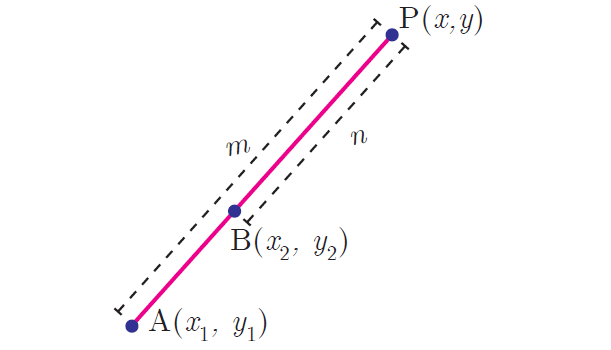
Let A(x₁, y₁) and B(x₂, y₂) be two distinct points such that point p(x, y) divides AB externally in the ratio m : n.

Then the coordinates of P are given by

Centroid of a Triangle :

The coordinates of the centroid (G) of a triangle with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are given by

Area of a Triangle :

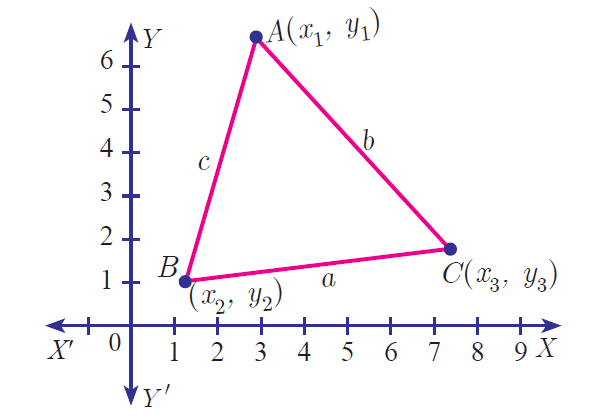
Area of a Triangle :

Let A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) be the vertices of a triangle.

Then the area of ΔABC is the absolute value of the expression :

The vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) of ΔABC are said to be “taken in order” if A, B, C are taken in counter-clock wise direction. If we do this, then area of DABC will never be negative.

Collinearity of three points :

Let A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) be the three distinct points. If these three points are collinear (lie on the same straight line), then ΔABC = 0.

That is,

Related Pages

• Area of triangle when vertices are given
• Area of triangle in coordinate geometry
• How to find area of triangle using coordinates

Area of a Quadrilateral :

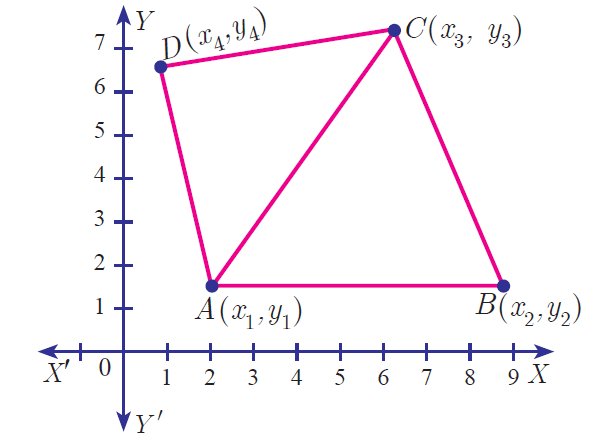
Let A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) and D(x₃, y₃) be the vertices of a quadrilateral.

Then the area of quadrilateral ABCD is

Related Pages

• Find area of quadrilateral with vertices
• Find area of quadrilateral with vertices
• Word problems to find area of quadrilaterals with vertices
• Area of triangle and quadrilateral with vertices worksheet

Slope of a straight line :

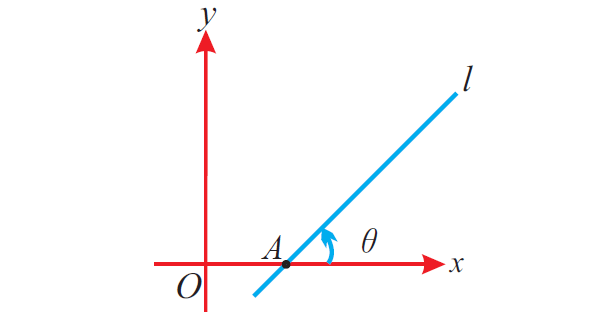
If θ is the angle of inclination of a non-vertical straight line, then tanθ is called the slope or gradient of the line and is denoted by m.

Therefore the slope of the straight line is

m = tanθ

Related Pages

• Finding slope and y-intercept from the given equation
• How to find the slope from an equation
• Write the equation of a line in standard form with one point and slope
• Practice questions on finding equations of line with point and slope
• Find the equation of a line given a point and the slope.
• Worksheet on finding slope from two points

Slope of a straight line when two points are given :

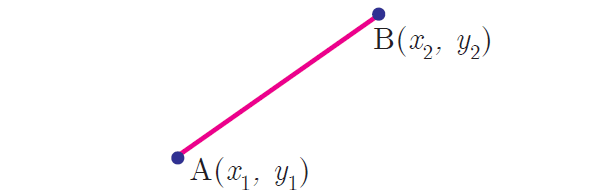
Let A(x₁, y₁) and B(x₂, y₂) be two distinct points on the line segment AB. Then, the slope of the line segment AB is

Related Pages

• Quiz on lines and slope
• Practice questions in slope and equation of lines
• Questions on slope and equation of a line for SAT
• Find slope x and y intercept for the given line worksheet

Slopes of parallel lines :

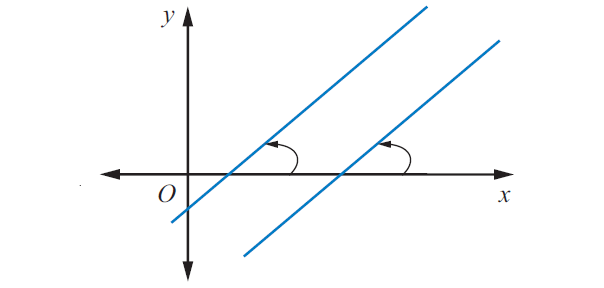
Let m₁ and m₂ be the slopes of two lines. If the two lines are parallel, then

m₁ = m₂

That is, if two lines are parallel, then the slopes are equal.

Related Pages

• Find slope x intercept and y intercept of the line
• Write the equation of a line from slope and y Intercept.
• The slope formula worksheet
• Comparing slopes of two lines
• Slopes of horizontal and vertical lines worksheet

Slopes of perpendicular lines :

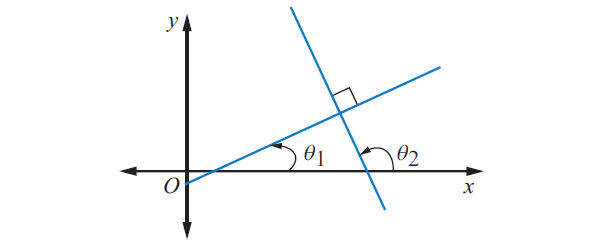
Let m₁ and m₂ be the slopes of two lines. If the two lines are perpendicular, then

m₁m₂ = -1

That is, if two lines are perpendicular, then the product of slopes equals to -1.

Equation of x-axis :

y = 0

Equation of y-axis :

x = 0

Equation of a straight line parallel to x-axis :

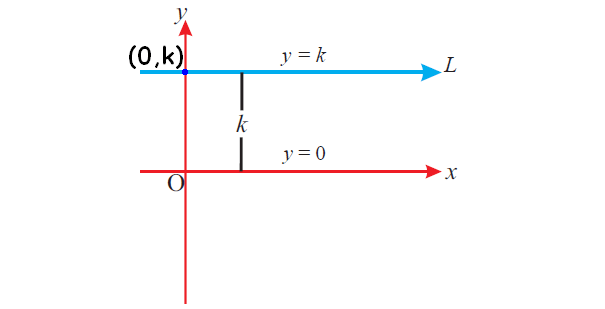
y = k

Equation of a straight line parallel to y-axis :

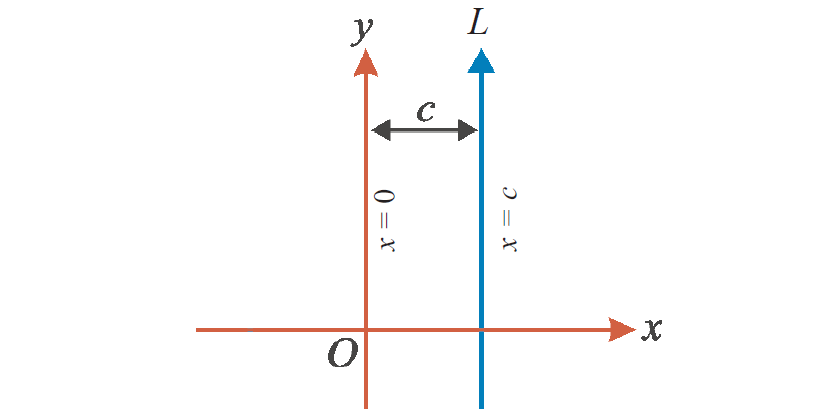
x = c

Equation of a line in general form :

Ax + By + C = 0

Equation of a line in standard form :

Ax + By = C

Equation of a line in slope-intercept form :

y = mx + b

where 'm' is the slope and 'b' is the y-intercept.

Equation of a line in point-slope form :

y - y₁ = m(x - x₁)

where 'm' is the slope and (x₁, y₁) is a point on the line.

Equation of a line in intercept form :

where 'a' is the x-intercept and 'b' is the y-intercept.

Angle between two straight lines :

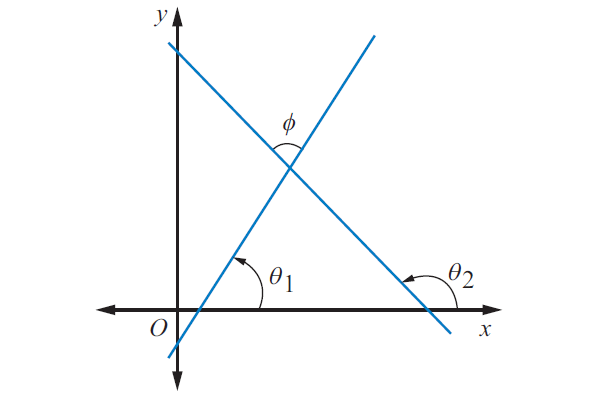
Let the equations of the two straight lines be

y = m₁x + b₁

y = m₂x + b₂

Then the angle between these two straight lines is

Related Pages

• Slopes of horizontal and vertical lines
• How to find slope and y intercept from an equation
• Find the slope from a graph
• Slope and graphing review
• Finding slope from a graph worksheet

Distance between a point and a line :

The distance from a point P(x₁, y₁) to a line ax + by + c = 0 is

Distance between two parallel lines :

Let the equations of two parallel lines be

ax + by + c₁ = 0

ax + by + c₂ = 0

Then the distance between these two parallel lines is

Related Pages

• Find the missing value if two lines are parallel or perpendicular.
• Parallel and perpendicular lines worksheet
• Parallel and perpendicular lines
• SAT math parallel and perpendicular lines
• Angle relationships in parallel lines and triangles worksheet

Equation of a circle in general form :

x² + y² + 2gx + 2fy + c = 0

where the center is C(-g, -f) and the radius is

Equation of a circle in standard form :

(x - h)² + (y - k)² = r²

where the center is C(h, k) and the radius is r.

Equation of a circle in standard form with center (0, 0) :

x² + y² = r²

Related Pages

• General form of equation of a circle
• Equation of a circle in standard form
• Writing equations of circles in standard form from graphs.
• Worksheet on equation of a circle in standard form
• Equation of a circle in standard form worksheet
• Finding the equation of a circle in general form

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.