GENERAL FORM OF EQUATION OF A CIRCLE

Example 1 : 

Write the following equation of a circle in general form. 

Solution :

(x + 4)² + y²  =  49

x² + 2(x)(4) + 4² + y²  =  49

x² + 8x + 16 + y²  =  49

x² + y² + 8x + 16  =  49

Subtract 49 from each side. 

x² + y² + 8x - 33  =  0

Example 2 : 

Write the standard equation of the circle whose general equation is

x² + y² - 4x + 6y - 12  =  0

Solution :

To find the standard equation of the circle, we need to know the center and radius. 

Let us find the center and radius from the given general equation of the circle. 

Comparing 

x² + y² + 2gx + 2fy + c  =  0

and

x² + y² - 4x + 6y - 12  =  0,

we have 

2g  =  - 4 -----> g  =  -2

2f  =  6 -----> f  =  3

c  =  -12

Center  =  (-g, -f)  =  (2, -3)

Radius  =  √[g² + f² - c]

Radius  =  √[(-2)² + 3² - (-12)]

Radius  =  √[4 + 9 + 12]

Radius  =  √25

Radius  =  5

Equation of the circle in standard form : 

(x - h)² + (y - k)²  =  r²

Substitute (h, k)  =  (2, -3) and r  =  5.

(x - 2)² + [y - (-3)²]  =  5²

(x - 2)² + (y + 3)²  =  25

Example 3 : 

Write the standard equation of the circle by completing the square method.

x² + y² - 6x + 8y - 12  =  0

Solution :

x² + y² - 6x + 8y - 12  =  0

x² - 6x + y² + 8y - 12  =  0

x² - 2(x)(3) + y² + 2(y)(4) - 12  =  0

x² - 2(x)(3) + 3² - 3² + y² + 2(y)(4) + 4² - 4² - 12  =  0

Using the expansions of (a - b)² and (a + b)²,

(x - 3)² - 3² + (y + 4)² - 4² - 12  =  0

(x - 3)² - 9 + (y + 4)² - 16 - 12  =  0

(x - 3)² + (y + 4)² - 37  =  0

(x - 3)² + (y + 4)²  =  37

Example 4 : 

If two end points of the diameter of a circle are (-1, -2) and (11, 14), find the equation of the circle in general form. 

Solution : 

Using mid point formula, find the mid point of the diameter.  

Mid point of (-1, -2) and (11, 14) : 

=  [(-1 + 11)/2, (-2 + 14)/2]

=  (10/2, 12/2)

=  (5, 6)

Mid point of the diameter is the center of the circle. 

So, the center of the circle is (5, 6). 

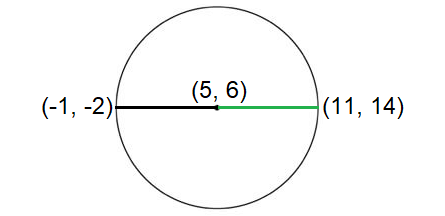
Using distance formula to find the distance between the center and one of the end points of the diameter.

Distance between (5, 6) and (11, 14) :

=  √[(11 - 5)² + (14 - 6)²]

=  √[6² + 8²]

=  √[36 + 64]

=  √100

=  10

Radius of the circle is 10 units. 

Equation of the circle in standard form : 

(x - h)² + (y - k)²  =  r²

Substitute (h, k) = (5, 6) and r = 10.

(x - 5)² + (y - 6)²  =  10²

Write the above equation of the circle in general form. 

(x - 5)² + (y - 6)²  =  10²

x² - 2(x)(5) + 5² + y² - 2(y)(6) + 6²  =  100

x² - 10x + 25 + y² - 12y + 36  =  100

x² + y² - 10x - 12y + 36  =  100

Subtract 100 from each side. 

x² + y² - 10x - 12y - 64  =  0

Example 5 : 

If the center and radius of the following equation of a circle are (2, -3) and 8, find the values of a, b and k. 

x² + y² + 16ax - 8by + k  =  0

Solution :

Comparing 

x² + y² + 2gx + 2fy + c  =  0

and

x² + y² + 16ax - 8by + k  =  0,

we have 

2g  =  16a -----> g  =  8a

2f  =  -8b -----> f  =  -4b

c  =  k

But, 

Center  =  (-g, -f)  =  (2, -3)

That is,

-g  =  2 -----> g  =  -2

-f  =  -3 -----> f  =  3

Then, 

Radius  =  8

√[g² + f² - c]  =  8

Square both sides. 

g² + f² - c  =  64

Substitute g = -2 and f = 3. 

(-2)² + 3² - c  =  64

4 + 9 - c  =  64

13 - c  =  64

Subtract 13 from each side.

-c  =  51

Multiply each side by -1.

c  =  -51

Example 6 : 

Write the standard equation of each circle.

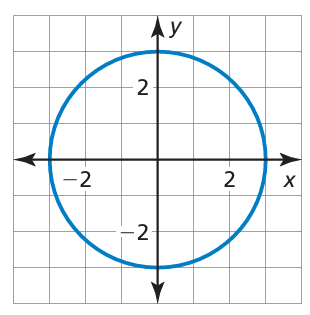
a. the circle shown below.

b. a circle with center (0, −9) and radius 4.2

Solution :

a) Center of the circle is at (0, 0) radius = 3 units

(x - h)² + (y - k)² = r²

(x - 0)² + (y - 0)² = 3²

x² + y² = 9

b) center (0, −9) and radius 4.2

(x - h)² + (y - k)² = r²

(x - 0)² + (y - (-9))² = 4.2²

x² + (y + 9)² = 17.64

Example 7 : 

The point (−5, 6) is on a circle with center (−1, 3). Write the standard equation of the circle.

Solution :

a) Center of the circle is at (-1, 3)

(x - h)² + (y - k)² = r²

(x - (-1))² + (y - 3)² = r²

(x + 1)² + (y - 3)² = r²

Since the point (-5, 6) lies on the circle,

(-5 + 1)² + (6 - 3)² = r²

(-4)² + 3² = r²

16 + 9 = r²

r² = 25

r = 5 units

Applying the value of r², we get

(x + 1)² + (y - 3)² = 25

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.