HOW TO FIND SLOPE AND Y INTERCEPT FROM AN EQUATION

The slope-intercept form of a line is :

y = mx + b

where m is the slope and b is the y-intercept.

Slope (m)  =   Rise / Run  =  Change in y/Change in x

The y-intercept is always where the line intersects the y-axis, and will always appear as (0, b) in coordinate form

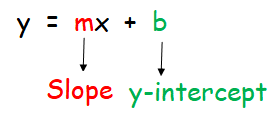
Example 1 :

Find the slope and y-intercept of the line whose equation is

(i)  y  =  x+1                    (ii) 5x  =  3y   

(iii) 4x–2y+1  =  0           (iv)  10x+15y+6  =  0

(i)  Answer :

To find slope and y-intercept of the given line we have to compare the equation with slope intercept formula

y  =  mx + b

y  =  x + 1

By comparing, we get

Slope (m)  =  1 and y-intercept (b)  =  1

(ii)  Answer :

5x  =  3y

3y  =  5x+0

y  =  (5/3)x + 0

By comparing, we get

Slope (m)  =  5/3 and y-intercept (b)  =  0.

(iii)  Answer :

4x–2y+1  =  0

2y  =  4x + 1

y  =  (4/2) x + 1/2

y  =  2x + 1/2

y  =  mx + b

By comparing, we get

Slope (m)  =  2 and y-intercept (b)  =  1/2.

(iv)  Answer :

10x+15y+6  =  0

15y  =  -10x-6

y  =  (-10/15)x–(6/15)

y  =  (-2/3)x-2/5

y  =  mx + b

By comparing, we get

Slope (m)  =  -2/3 and y-intercept (b)  =  -2/5.

Example 2 :

For the function f, the graph of y = f (x) in the xy-plane has a slope of 3 and passes through the point (0, −8). Which equation defines f ?

A) f (x) = 3x              B) f (x) = 3x − 8

C) f (x) = 3x + 5        D) f (x) = 3x + 11

Solution :

Slope = 3, the point on the line is (0, -8)

Slope intercept form :

y = mx + b

Applying slope, we get 

y = 3x + b ---(1)

Applying the point (0, -8), we get the value of b.

-8 = 3(0) + b

-8 = b

y = 3x - 8

So, the required equation is y = 3x - 8.

Example 3 :

A model predicts that a certain animal weighed 241 pounds when it was born and that the animal gained 3 pounds per day in its first year of life. This model is defined by an equation in the form f (x) = a + bx, where f (x) is the predicted weight, in pounds, of the animal x days after it was born, and a and are constants. What is the value of a ?

Solution :

Initial weight = 241 pounds

weight gain each day = 3 pounds

f(x) = 3x + 241

Comparing with f(x) = a + bx

Then the value a is 241.

Example 4 :

Line k is defined by y = (1/4) x + 1. Line j is parallel to line k in the xy-plane. What is the slope of j ?

Solution :

Equation of k :

y = (1/4) x + 1

Equation of j :

Since lines k and j are parallel, they will have same slope. So, the slope of the line j is 1/4.

Example 5 :

When the equation y = 5x + p, where p is a constant, is graphed in the xy-plane, the line passes through the point (−2, 1). What is the value of p ?

A) −9      B) −2        C) 3           D) 11

Solution :

Since (-2, 1) is one of the points lie on the line y = 5x + p, the line will satisfy the point given.

1 = 5(-2) + p

1 = -10 + p

1 + 10 = p

p = 11

So, the value of p is 11.

Example 6 :

The equation y = 36 + 18x models the relationship between the height y, in inches, of a typical golden delicious apple tree and the number of years, x, after it was planted. If the equation is graphed in the xy-plane, what is indicated by the y-intercept of the graph?

A) The age, in years, of a typical apple tree when it is planted

B) The height, in inches, of a typical apple tree when it is planted

C) The number of years it takes a typical apple tree to grow

D) The number of inches a typical apple tree grows each year

Solution :

y = 36 + 18x

x is the number of years after it planted 

To find y-intercept, we apply x = 0

y = 36 + 18(0)

y = 36

Here y represents the height of the tree in inches.

So, the answer is option B,  the height, in inches, of a typical apple tree when it is planted.

Example 7 :

A line is graphed in the xy-plane. If the line has a positive slope and a negative y-intercept, which of the following points cannot lie on the line?

A) (−3, −3)     B) (−3, 3)      C) (3, −3)       D) (3, 3)

Solution :

If the line has a positive slope, then it must be raising line. If it has negative y- intercept, it may lie below the x-axis.  So, the required line will lie in the 1st, 3rd and 4th quadrants.

It will not lie in the second quadrant. All the points in the second quadrant will be in the form (-x, y). So, option B is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.