FINDING SLOPE AND Y INTERCEPT FROM THE GIVEN EQUATION

Question 1 :

Find the slope and y-intercept of the line whose equation is y = x + 1.

Solution : 

To find the slope and y-intercept of any line, we have to compare the given equation with y = mx + c.

Here m stands for slope and c stands for y-intercept.

y = x + 1

y = mx + c

Comparing y = x  + 1 to y = mx + c, we get

slope (m)  =  1

y-intercept (c)  =  1

Question 2 :

Find the slope and y-intercept of the line whose equation is 5x = 3y.

Solution :

3y  =  5x 

y = (5/3)x

Then,

Slope (m)  =  5/3

y-intercept (c)  =  0

Question 3 :

Find the slope and y-intercept of the line whose equation is 4x - 2y + 1 = 0

Solution :

2y = 4x + 1

y = (4/2)x + (1/2) 

y = 2 x + (1/2)

Then,

slope (m)  =  2

y-intercept (c)  =  1/2

Question 4 :

Find the slope and y-intercept of the line whose equation is 10x + 15y + 6 = 0.

Solution :

15y = -10x - 6 

y = (-10/15)x - (6/15) 

y = (-2/3) x - (2/5)

Then,

slope m  =  -2/3

y-intercept (c)  =  2/5

Question 5 :

Find the equation of the straight line whose slope is -4 and passing through (1, 2).

Solution :

Slope (m)  = -4  and  (x₁, y₁)  =  (1, 2).

(y - y₁)  =  m(x - x₁)

(y - 2)  =  -4(x - 1)

y - 2  =  -4x + 4 

4x + y - 2 - 4  =  0

4x + y - 6  =  0

Question 6 :

Find the equation of the straight line whose slope slope is 2/3 and passing through (5, -4).

Solution :

Slope (m)  =  2/3, (x₁, y₁)  =  (5, -4).

(y - y₁)  =  m (x - x₁)

(y - (-4)) =  (2/3)(x - 5)

(y + 4) = (2/3) (x - 5)

3(y + 4) = 2(x - 5)

3y + 12 = 2x - 10

2x - 3y - 10 - 12 = 0

2x - 3y - 22 = 0

Question 7 :

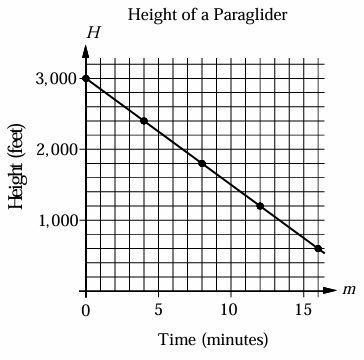
The graph above shows the relationship between the height of paraglider H, in feet, and time m, in minutes.

Which of the following represents the relationship between H and m? 

A) H(m) = -100m + 3000       B)  H(m) = -150m + 3000

C)  H(m) = -175m + 3000      D)   H(m) = -225m + 3000

Solution :

By observing the graph above, the y-intercept is 3000.

Choosing two points from the line,

(8, 1800) and (14, 1200)

Slope = (1200 - 1800) / (14 - 8)

= -600/6

= -100

Equation of the line :

y = -100m + 3000

Question 8 :

From the graph give above, if the height of the paraglider is 1,350 feet, which of the following best approximates the time the paraglider has been flying?

A) 10 minutes       B) 10 minutes and 30 seconds

C) 11 minutes        D) 11 minutes and 30 seconds

Solution :

By drawing the horizontal line, we get 11 minutes and 30 seconds.

Question 9 :

A line in the xy plane passes through the point (1, -2) and has a slope of 1/3 .Which of the following points lies on the line?

A) (3, 2)      B) (2, -4/3)     C) (0, 2)      D) (-1, -8/3)

Solution :

Slope = 1/3

One of the points on the line is (1, -2).

Equation of line :

(y - y₁) = m(x - x₁)

(y + 2) = (1/3)(x - 1)

3(y + 2) = x - 1

3y + 6 = x - 1

x - 3y - 1 - 6 = 0

x - 3y = 7

To check if the points lie on the line, we have to apply

So, point D lies on the line.

Question 10 :

If the slope of the line in the xy plane that passes through the points (2, -4) and (6, k) is 3/2 , what is the value of k?

Solution :

Slope of the line joining two point (2, -4) and (6, k)

slope = (k - (-4)) / (6 - 2)

= (k + 4) / 4

Slope given = 3/2

(k + 4) / 4 = 3/2

2(k + 4) = 3(4)

2k + 8 = 12

2k = 12 - 8

2k = 4

k = 4/2

k = 2

So, the value of k is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.