SAT MATH - PARALLEL AND PERPENDICULAR LINES

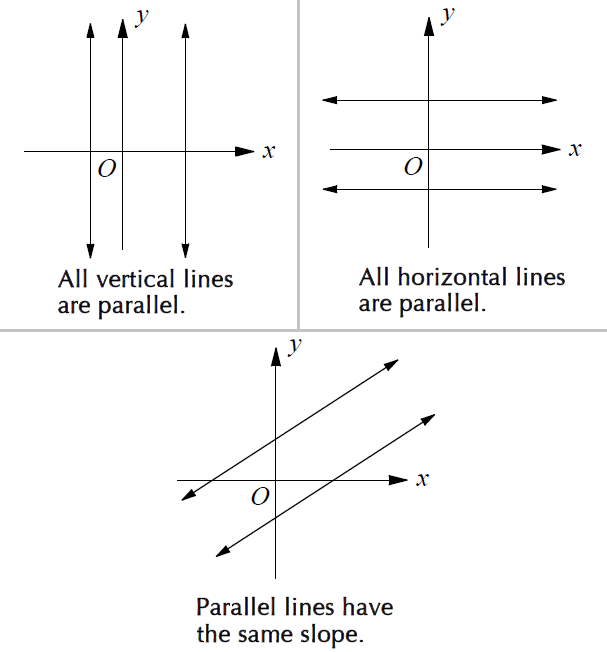
Parallel Lines

Lines in the same plane that do not intersect are called parallel lines. Parallel lines have the same slope. If two nonvertical lines have the same slope, then they are parallel.

Parallel Lines in a Coordinate Plane

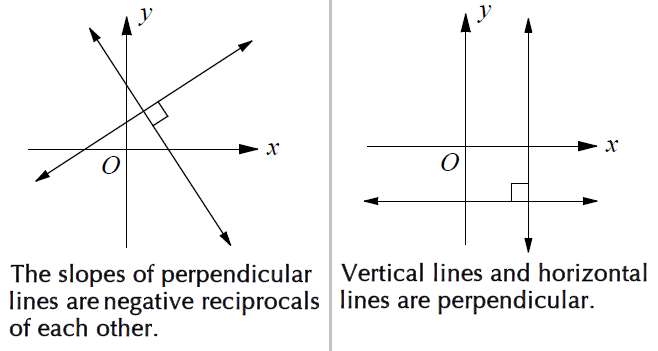
Perpendicular Lines

Lines that intersect at right angles are called perpendicular lines. If the product of the slopes of two non-vertical lines is -1, then the lines are perpendicular.

Perpendicular Lines in a Coordinate PlaneThe

Solved Problems

Problem 1 :

Write the equation in point-slope form of the lines through point (1, 2) that are

(a) parallel to 3x - y + 2 = 0

(b) perpendicular to 3x - y + 2 = 0.

Solution :

Part (a) :

Write the equation 3x - y + 2 = 0, in slope-intercept form.

3x - y + 2 = 0

Add y to both sides.

3x + 2 = y

y = 3x + 2

Comapring the above equation to y = mx + b,

slope m = 3

Equation of a line in point-slope form :

y - y₁ = m(x - x₁)

Parallel lines have the same slope.

Substitute m = 3 and (x₁, y₁) = (1, 2) into point-slope of equation of a line.

y - 2 = 3(x - 1)

Part (b) :

The line perpendicular to y = 3x + 2 has a slope of -⅓ which is negative reciprocal of 3.

Substitute m = -⅓ and (x₁, y₁) = (1, 2) into point-slope of equation of a line.

y - 2 = (⅓)(x - 1)

Problem 2 :

Which of the following equations represents a line that is parallel to the line with equation y = -½x + 5 and contains the point (-2, ½)?

(A)  x - 2y = -3

(B)  x + 2y = -1

(C)  2x - y = -5

(D)  2x + y = -3

Solution :

y = -½x + 5

Parallel lines have the same slope.

Substitute m = -½ and (x₁, y₁) = (-2, ½) into point-slope of equation of a line.

y - ½ = -½[x - (-2)]

y - ½ = -½(x + 2)

Multiply both sides by 2.

2(y - ½) = 2[-½(x + 2)]

2y - 2(½) = -1(x + 2)

2y - 1 = -x - 2

x + 2y = -1

Therefore, the correct answer is option (B).

Problem 3 :

Which of the following equations represents a line that passes through (7,6) and is parallel to the -xaxis?

(A)  x = 6

(B)  y = 7

(C)  y = 7

(D)  y = 6

Solution :

A line parallel to x-axis is an horizontal line. An horizontal line always has a slope of 0.

So, the required passes through the point (7, 6) with a slope of 0.

Substitute m = 0 and (x₁, y₁) = (7, 6) into point-slope of equation of a line.

y - 6 = 0(x - 7)

y - 6 = 0

y = 6

Therefore, the correct answer is option (D).

Problem 4 :

Which of the following equations represents a line that passes through (-5, 1) and is parallel to the -yaxis?

(A)  y = -5

(B)  y = 1

(C)  x = -5

(D)  x = 1

Solution :

A line parallel to y-axis is a vertical line. The slope of a vertical line always undefined. When a non-zero number is divided by zero, it is undefined. So, ¹⁄₀ can be considered as the slope of a vertical line.

So, the required passes through the point (-5, 1) with a slope of ¹⁄₀.

Substitute m = ¹⁄₀ and (x₁, y₁) = (-5, 1) into point-slope of equation of a line.

y - 1 = ¹⁄₀[x - (-5)]

0(y - 1) = 1[x - (-5)]

0 = x + 5

x = -5

Therefore, the correct answer is option (C).

Problem 5 :

A line passes through the points (-1, 2) and (5, k), and is parallel to the graph of the equation 4x - 2y = 13. Find the value of k.

Solution :

Formula to find the slope of a line joining two points :

Substitute (x₁, y₁) = (-1, 2) and (x₂, y₂) = (5, k).

Slope of the line joining the points (-1, 2) and (5, k) is

= ⁽ᵏ ⁻ ²⁾⁄₆ ----(1)

Write the equation 4x - 2y = 13 in slope-intercept form.

4x - 2y = 13

Subtract 4x from both sides.

-2y = -4x + 13

Multiply both sides -1.

2y = 4x - 13

Divide both sides by 2.

y = 2x - 6.5

Comparing the above equation to y = mx + b,

slope m = 2 ----(2)

We already know that parallel lines have the same slope.

(1) = (2)

⁽ᵏ ⁻ ²⁾⁄₆ = 2

Multiply both sides by 6.

k - 2 = 12

Add 2 to both sides.

k = 14

Problem 6 :

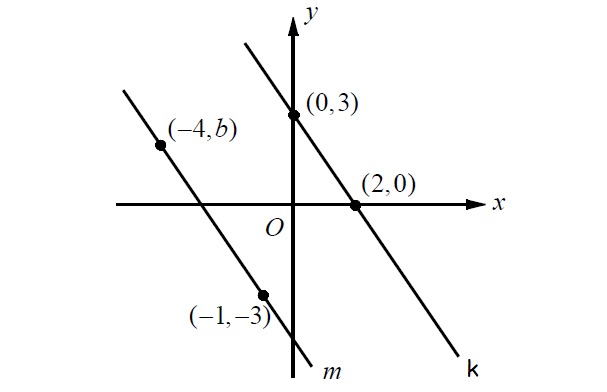
In the xy-plane above, if line k is parallel to line m, find the value of b. 

Solution :

Formula to find the slope of a line joining two points :

Slope of the line m :

Substitute (x₁, y₁) = (-1, -3) and (x₂, y₂) = (-4, b) into the above formula.

Slope of the line k :

Substitute (x₁, y₁) = (2, 0) and (x₂, y₂) = (0, 3) into the above formula.

Since the lines m and k are parallel, the slopes must be equal.

(1) = (2)

⁽^b ⁺ ³⁾⁄₋₃ = -³⁄₂

By cross multiplication,

2(b + 3) = -3(-3)

2b + 6 = 9

Subtract 6 from both sides.

2b = 3

Divide both sides by 2.

b = ³⁄₂

Problem 7 :

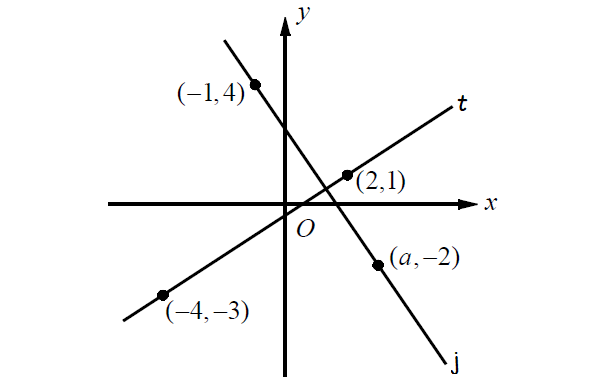
In the xy-plane above, if line t is parallel to line j, find the value of a. 

Solution :

Formula to find the slope of a line joining two points :

Slope of the line j :

Substitute (x₁, y₁) = (a, -2) and (x₂, y₂) = (-1, 4) into the above formula.

Slope of the line t :

Substitute (x₁, y₁) = (-4, -3) and (x₂, y₂) = (2, 1) into the above formula.

Since the lines j and t are perpendicular, the product of the slopes must be equal to -1.

(1) ⋅ (2) = -1

Take reciprocal on both sides.

⁽¹ ⁺ ᵃ⁾⁄₄ = 1

Multiply both sides by 4.

1 + a = 4

Subtract 1 from both sides.

a = 3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.