FIND THE MISSING VALUE IF TWO LINES ARE PARALLEL OR PERPENDICULAR

Question 1 :

Find the slope of the straight line

(i) 3x + 4y -6 = 0

Answer :

Slope (m)  =  - Coefficient of x/coefficient of y

 =  -3/4

(ii)  y  =  7x + 6

Answer :

y = 7 x + 6

By comparing the given equation with slope intercept form (y = mx + b), we get 

Slope  =  7

(iii)  4 x = 5y + 3

Answer :

4 x - 5 y - 3 = 0

Slope (m) = - coefficient of x/coefficient of y

  =  -4/(-5)  =  4/5

Question 2 :

Show that the straight lines x + 2 y + 1 = 0 and 3x + 6y + 2 = 0 are parallel

Answer :

Since the given lines are parallel, m₁ = m₂

Slope of the first line x + 2 y + 1 = 0

Slope (m)  =  - coefficient of x/coefficient of y

m₁  =  -1/2  ----(1)

Slope of the second line 3x + 6y + 2 = 0

m₂ = -3/6  =  -1/2  ----(2)

(1)  =  (2)

Then the given lines are parallel.

Question 3 :

Show that the straight lines 3x – 5y + 7 = 0 and 15 x + 9y + 4 = 0 are perpendicular.

Answer :

If two lines are perpendicular then

m₁ x m₂ = -1

Slope of the first line 3x - 5 y + 7 = 0

Slope (m) = - coefficient of x/coefficient of y

m₁  = -3/(-5)

  = 3/5  

Slope of the second line 15x + 9y + 4 = 0

m₂  =  -15/9  = -5/3

m₁ ⋅ m₂ = (3/5) x (-5/3)  =  -1

Hence the given lines are perpendicular.

Question 4 :

If the straight lines y/2 = x – p and ax + 5 = 3y are parallel, then find a.

Answer :

(1)  =  (2)

2  =  a/3

a  =  6

Question 5 :

Find the value of a if the straight lines 5x – 2y – 9 = 0 and ay + 2x – 11 = 0 are perpendicular to each other.

Answer :

m₁ ⋅ m₂ = -1

(5/2) ⋅ (-a/2) = -1

-5a/4 = -1

5 a = 4

a = 4/5

Question 6 :

• The line Q passes through the points (−10, −2) and (−8, −8)
• The line R passes through the points (1, 2) and (10, a)

The lines Q and R are perpendicular. Find the value of a

Answer :

The lines P and Q are perpendicular to each other.

Slope of the line P = (-8 - (-2))/(-8 - (-10))

= (-8 + 2)/(-8 + 10)

= -6/2

= -3

Slope of the line Q = (a - 2) / (10 - 1)

= (a - 2) / 9

Product of the slopes = -1

-3 ⋅ (a - 2) / 9 = -1

a - 2 = 3

a = 3 + 2

a = 5

So, the value of a is 5.

Question 7 :

A line passes through the points (-1, 2) and (5, b) and is parallel to the graph of the equation 4x - 2y = 13, what is the value of b ?

Answer :

If two lines are parallel, then slopes will be equal

Slope of the line passes through the points (-1, 2) and (5, b)

= (b - 2) / (5 - (-1))

= (b - 2) / (5 + 1)

= (b - 2) / 6

Slope of the line 4x - 2y = 13

2y = 4x - 13

y = (4x/2) - 13/2

y = 2x - (13/2)

Slope = 2

(b - 2) / 6 = 2

b - 2 = 2(6)

b - 2 = 12

b = 12 + 2

b = 14

So, the value of b is 14.

Question 8 :

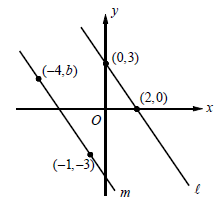
In the xy-plane above, line l is parallel to line m. What is the value of b?

Answer :

Since the shown lines are parallel, they will have same slope.

Slope of line passes through the points (-4, b) and (-1, -3)

= (-3 - b) / (-1 -(-4))

= (-3 - b) / (-1 + 4)

= (-3 - b) / 3 ------(1)

Slope of the line passes through the points (0, 3) and (2, 0)

= (0 - 3) / (2 - 0)

= -3/2 ---------(2) 

(-3 - b) / 3 = -3/2

(3 + b) / 3 = 3/2

2(3 + b) = 3(3)

6 + 2b = 9

2b = 9 - 6

2b = 3

b = 3/2

So, the value of b is 3/2.

Question 9 :

In the system of equations above, a and b are constants and x and y are variables. If the system of equations  above has no solution, what is the value of a⋅b?

ax - y = 0

x -  by = 1

Answer :

ax - y = 0

x -  by = 1

When the system of equation has no solution, they must be parallel and they will have same slope.

y = ax

Slope = a

by = x - 1

y = (1/b) x - (1/b)

Slope = 1/b

a = 1/b

a⋅b = 1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.