LOGARITHM QUESTIONS AND ANSWERS CLASS 11

Problem 1 :

Let b > 0 and b ≠ 1. Express y = b^x in logarithmic form. Also state the domain and range of the logarithmic function. 

Solution :

Problem 2 :

Compute :

log₉ 27 − log₂₇ 9

Solution :

Problem 3 :

Solve :

log₈ x + log₄ x + log₂ x = 11

Solution :

Problem 4 :

Solve :

log₄ 2^8x = 2^log₂ ⁸

Solution :

Problem 5 :

If a² + b² = 7ab, show that log(a + b)/3 = 1/2(log a + log b)

Solution :

Problem 6 :

Prove that

log (a²/bc) + log (b²/ac) + log (c²/ab) = 0

Solution :

Problem 7 : 

Prove that

log 2 + 16log (16/15) + 12log (25/24) + 7log(81/80) = 1

Solution :

Problem 8  : 

Prove that 

Solution :

Problem 9 :

Prove :

log a + log a² + log a³ + · · · + log aⁿ = [n(n + 1)/2]log a

Solution :

Problem 10 :

If log x/(y - z)  =  log y/(z - x)  =  log z/(x - y), then prove that xyz  =  1.

Solution :

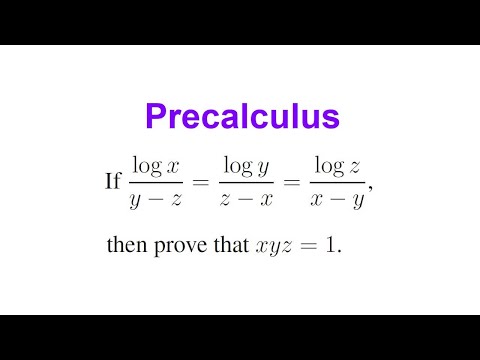
Problem 11 :

Solve :

log₂ x − 3log_1/2 x  =  6

Solution :

Problem 12 :

Solve :

log_5-x (x² − 6x + 65) = 2

Solution :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.