WRITE THE EQUATION OF A LINE FROM SLOPE AND Y INTERCEPT

Find the equation from the given gradient and y-intercept.

Example 1 :

Gradient  =  2 and y – intercept  =  7

Solution :

Gradient(m)  =  2

y – intercept(b)  =  7

Equation of a straight line y  =  mx + b

y  =  2x + 7

So, the required equation is y  =  2x + 7

Example 2 :

Gradient  =  4 and y – intercept  =  -6

Solution :

Gradient(m)  =  4

y – intercept(b)  =  - 6

Equation of a straight line y  =  mx + b

y  =  4x - 6

So, the required equation is y  =  4x – 6

Example 3 :

Gradient  =  -3 and y – intercept  =  -1

Solution :

Gradient(m)  =  - 3

y – intercept(b)  =  - 1

Equation of a straight line y  =  mx + b

y  =  -3x - 1

So, the required equation is y  =  -3x – 1

Example 4 :

Gradient  =  – 1/2 and y – intercept  =  2

Solution :

Gradient m  =  - 1/2

y – intercept b  =  2

Equation of a straight line y  =  mx + b

y  =  (-1/2)x + 2

So, the required equation is y  =  (-1/2)x + 2.

Example 5 :

Gradient  =  0 and y – intercept  =  8

Solution :

Gradient(m)   =  0

y – intercept(b)  =  8

Equation of a straight line y  =  mx + b

y  =  0x + 8

So, the required equation is y  =  8.

Example 6 :

Undefined gradient, through (2, 5)

Solution :

Gradient(m)  =  1/0

By using slope point formula,

(y – y₁)  =  m (x – x₁)

Since the given line is passing through the point (2, 5)

(2, 5)------>(x₁, y₁)

(y – 5)  =  1/0 (x – 2)

0  =  1 (x – 2)

x – 2  =  0

x  =  2

So, the required equation is x  =  2.

Example 7 :

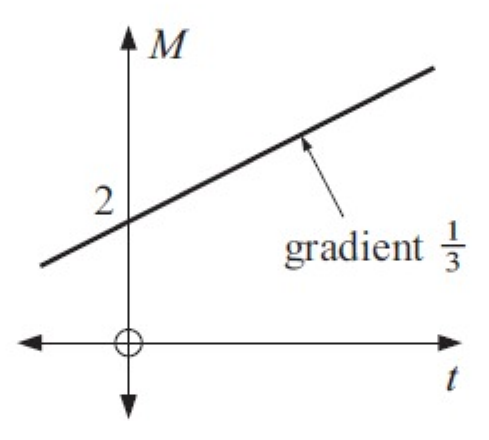
Solution :

Slope of a line  =  1/3

y – intercept(b)  =  2

Equation of a straight line y  =  mx + b

y  =  1/3x + 2

3y  =  x + 6

x – 3y + 6  =  0

So, the required equation is x – 3y + 6  =  0.

Example 8 :

A line has equation y = 2x + 6

• The line crosses the x−axis at the point A
• The line crosses the y−axis at the point B
• The point C has coordinates (1, 8)

(a) Find the coordinates of the point A

(b) Find the coordinates of the point B

(c) Find the equation of the straight line passing through the points A and C.

Solution :

y = 2x + 6

a)  To find the x-intercept, we put y = 0

0 = 2x + 6

2x = -6

x = -6/2

x = -3

Coordinate A (-3, 0)

b)  To find the y-intercept, we put x = 0

y = 2(0) + 6

y = 0 + 6

y = 6

Coordinate B(0, 6)

c)  Equation of line passes through A and C :

A (-3, 0) and C (1, 8)

(y – y₁)  =  m (x – x₁)

Slope (m) = (y₂ - y₁)/(x₂ - x₁)

= (8 - 0) / (1 + 3)

= 8/4

= 2

y - 0 = 2(x - (-3))

y = 2(x + 3)

y = 2x + 6

Example 9 :

Do the lines y = 3x + 1 and 4x − 2y + 3 = 0 have the same gradients?

Solution :

y = 3x + 1

Slope of the line comparing with y = mx + b

Slope (m) = 3

4x − 2y + 3 = 0

Slope of the line by converting this equation into slope intercept form.

2y = 4x + 3

y = (4x/2) + (3/2)

y = 2x + (3/2)

Slope (m) = 2

So, the lines donot have same slope.

Example 10 :

Line 1 has equation y = 3x − 12

(a) Find the coordinates of P

(b) Find the equation of line 2.

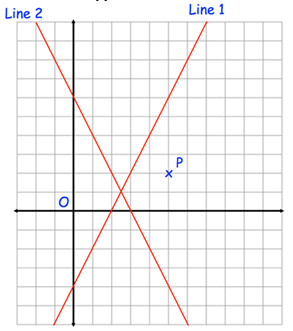
Solution :

a) The point P is (5, 2).

b) Equation of line 2 :

From y-intercept of line 2,

Run = 3 and run = -6

Slope = rise / run 

= 3/(-6)

= -1/2

y-intercept = 6

y = mx + b

y = (-1/2)x + 6

y = -x/2 + 6

y = (-x + 12)/2

2y = -x + 12

x + 2y = 12

So, the required equation is x + 2y = 12.

Example 11 :

Lexi says the line below has an equation of y = −2x + 8 Explain her mistake

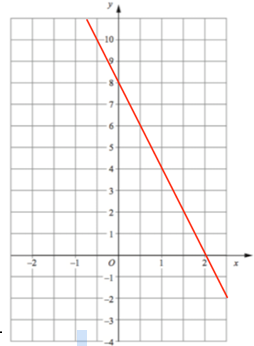
Solution :

From the graph of line given above, y-intercept = 8

Rise = -8 and run = 4

Equation of line :

Slope = rise / run

= -8/4

= -2

y = mx + b

y = -2x + 8

She has got correct answers.

Example 12 :

What is the equation of the line that passes through the point (0, 5) and is parallel to the graph of

y = 7x + 4

in the xy-plane?

A) y = 5x    B) y = 7x + 5    C) y = 7x    D) y = 5x + 7

Solution :

Since the given line is parallel to y = 7x + 4

comparing with y = mx + b

m = 7

Equation of the line passes through (0, 5) and slope = 7

y - y1 = m(x - x1)

y - 5 = 7(x - 0)

y - 5 = 7x

y = 7x + 5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.