AREA OF TRIANGLE WHEN VERTICES ARE GIVEN

Here, we are going to see, how to find area of a triangle when coordinates of the three vertices are given. 

Let us consider the triangle given below. 

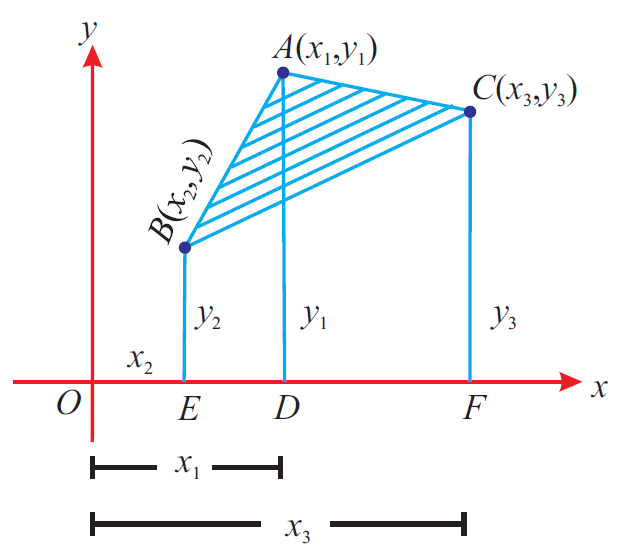
In the above triangle, A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are the vertices.

To find area of the triangle ABC, now we have take the vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) of the triangle ABC in order (counter clockwise direction) and write them column-wise as shown below. 

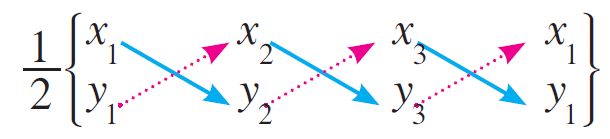
And the diagonal products x₁y₂, x₂y₃ and x₃y₁ as shown in the dark arrows. 

Also add the diagonal products x₂y₁, x₃y₂ and x₁y₃ as shown in the dotted arrows.

Now, subtract the latter product from the former product to get area of the triangle ABC.

So, area of the triangle ABC is

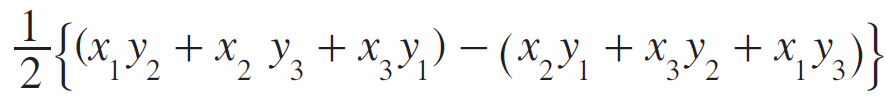
Condition for Three Points to be Collinear

Three or more points in a plane are said to be collinear, if they lie on the same straight line.

In other words, three points A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are collinear, if any one of these points lies on the straight line joining the other two points. 

Suppose that the three points A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are collinear, then they can not form a triangle. So, the area of triangle ABC  is equal to zero.

That is, 

1/2 ⋅ {(x₁y₂ + x₂y₃ + x₃y₁) - (x₂y₁ + x₃y₂ + x₁y₃)}  =  0

or

(x₁y₂ + x₂y₃ + x₃y₁  =  x₂y₁ + x₃y₂ + x₁y₃

One can prove that the converse is also true.

So, the area of triangle ABC is zero, if and only if the points A, B and C are collinear.

Solved Problems

Problem 1 :

Find the area of the triangle whose vertices are (1, 2), (-3, 4) and (-5, -6)

Solution :

Plot the given points in a rough diagram as given below and take them in order (counter clock wise)

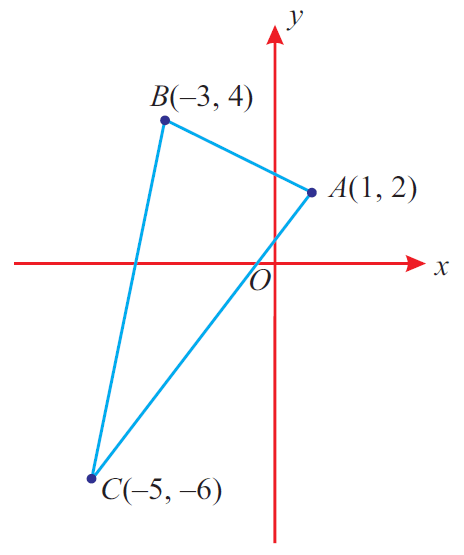
Let the vertices be A(1, 2), B(-3, 4) and C(-5, -6)

Then, we have 

(x₁, y₁)  =  (1, 2)

(x₂, y₂)  =  (-3, 4)

(x₃, y₃)  =  (-5, -6)

Area of triangle ABC is 

=  1/2 ⋅ {(x₁y₂ + x₂y₃ + x₃y₁) - (x₂y₁ + x₃y₂ + x₁y₃)}

=  (1/2) ⋅ {[(1)(4) + (-3)(-6) + (-5)2] - [(-3)2 + (-5)4 + 1(-6)]}

=  (1/2) ⋅ { [4 + 18 - 10] - [-6 - 20 -6] }

=  (1/2) x  { [12] - [-32] }

=  (1/2) x  { 12 + 32 }

=  (1/2) x  {  44 }

=  22 square units. 

So, area of the triangle ABC is 22 square units.

Problem 2 :

If the area of the triangle ABC is 68 square units and the vertices are A(6, 7), B(-4, 1) and C(a, -9) taken in order, then find the value of "a".  

Solution :

Let 

(x₁, y₁)  =  (6, 7)

(x₂, y₂)  =  (-4, 1)

(x₃, y₃)  =  (a, -9) 

Given :  Area of triangle ABC is 68 square units.

Then,

1/2 ⋅ {(x₁y₂ + x₂y₃ + x₃y₁) - (x₂y₁ + x₃y₂ + x₁y₃)}  =  68

Multiply each side by 2

{(x₁y₂ + x₂y₃ + x₃y₁) - (x₂y₁ + x₃y₂ + x₁y₃)}  =  136

{[6 + 36 + 7a] - [-28 + a - 54]}  =  136

 [42 + 7a] - [a - 82]  =  136

42 + 7a -a +82  =  136

6a + 124  =  136

6a  =  12

a  =  2

Problem 3 :

Using the concept of area of triangle, show that the points A(5, -2), B(4, -1) and C(1, 2) are collinear.

Solution :

Let 

(x₁, y₁)  =  (5, -2)

(x₂, y₂)  =  (4, -1)

(x₃, y₃)  =  (1, 2)

x₁y₂ + x₂y₃ + x₃y₁  =  5(-1) + 4(2) + 1(-2)

x₁y₂ + x₂y₃ + x₃y₁  =  -5 + 8 -2

x₁y₂ + x₂y₃ + x₃y₁  =  1 -----(1)

x₂y₁ + x₃y₂ + x₁y₃  =  4(-2) + 1(-1) + 5(2)

x₂y₁ + x₃y₂ + x₁y₃  =  -8 -1 + 10

x₂y₁ + x₃y₂ + x₁y₃  =  1 -----(2)

From (1) and (2), we get 

x₁y₂ + x₂y₃ + x₃y₁  =  x₂y₁ + x₃y₂ + x₁y₃

So, the three points A, B and C are collinear. 

Problem 4 :

If P(x, y) is any point on the line segment joining the points (a, 0), and (0, b), then prove that x/a + y/b  =  1. where  a ≠ b. 

Solution :

Clearly, the points (x, y), (a, 0), and (0, b) are collinear. 

Then,

area of the triangle  =  0 

Because area of the triangle is zero, we have

x₁y₂ + x₂y₃ + x₃y₁  =  x₂y₁ + x₃y₂ + x₁y₃ -----(1)

Here,

(x₁, y₁)  =  (x, y)

(x₂, y₂)  =  (a, 0)

(x₃, y₃)  =  (0, b)

(1)-----> x ⋅ 0 + a ⋅ b + 0 ⋅ y  =  a ⋅ y + 0 ⋅ 0 + x ⋅ b

0 + ab + 0   =   ay + 0 + xb

 ab   =   ay + xb

Divide each side by ab.

1  =  y/b + x/a

or 

x/a + y/b  =  1

Problem 5 :

If the points (k, -1), (2, 1) and (4, 5) are collinear, then find the value of "k".  

Solution :

Because the given points are collinear,

area of triangle  =  0 

Then, we have

x₁y₂ + x₂y₃ + x₃y₁  =  x₂y₁ + x₃y₂ + x₁y₃ -----(1)

Here,

(x₁, y₁)  =  (k, -1)

(x₂, y₂)  =  (2, 1)

(x₃, y₃)  =  (4, 5)

(1)-----> k(1) + 2(5) + 4(-1)  =  2(-1) + 4(1) + k(5)

k + 10 - 4  =  -2 + 4 + 5k

k + 6   =   2 + 5k

4  =  4k

1  =  k

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.