QUESTIONS ON SLOPE AND EQUATION OF A LINE FOR SAT

Question 1 :

In the xy‑plane above, a point (not shown) with coordinates (a, b) lies on the graph of the linear function h.

If a and b are positive integers, what is the ratio of a to b?

A) 2:3    B) 3:2    C) 5:6     D) 6:5

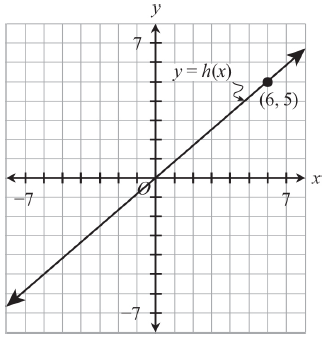
Solution :

The line passes through the point (0, 0), the point (6, 5) is compared with a, b, then 6 : 5 is the answer. Option D.

Question 2 :

A line that passes through the origin in the xy-plane has a
slope of 7/3. Which of the following is a point on the line?

A) (−14, −6)       B) (−6,−14)    C) (−6, 14)     D) (14, 6)

Solution :

From the information, we know that one of the points on the line is at origin (0, 0).

Let the required point be (x, y)

(y₂ - y₁) / (x₂ - x₁) = 7/3

(y - 0) / (x - 0) = 7/3

y/x = 7/3

Considering option A,

(-14, -6) ==> -6/-14 ==> 3/7

Then, option A is incorrect.

Considering option A,

(-6, -14) ==> -14/-6 ==> 7/3

Then, option B is correct.

Question 3 :

Sara is waiting in line to ride the amusement park’s newest roller coaster. The number of people in front of her can be represented by the equation

P = 34 − 2m

where P is the number of people in front of her and m is the number of minutes Sara has waited in line. What is the meaning of the value 34 in this equation?

A) Sara will reach the front of the line within 34 minutes.

B) Sara started with 34 people in front of her.

C) Sara moves up in the line at a rate of 34 people per hour.

D) Sara moves up in the line at a rate of 34 people per minute.

Solution :

P = 34 − 2m

Comparing with y = mx + b, slope = -2 and y-intercept = 34

• P = the number of people in front of her
• m = the number of minutes Sara has waited in line

Number of people waited in front of her = 34.

So, option B is correct.

Question 4 :

A line passes through the origin and points (−4, c) and (c, −9). What is one possible value of c?

A) 4     B) 6    C) 9    D) 12

Solution :

slope of the line passes through the points (0, 0) and (-4, c) = Slope of the line passes through (0, 0) and (c, -9)

(c - 0) / (-4 - 0) = (-9 - 0) / (c - 0)

-c/4 = 9/c

c² = 36

c = 6

So, the value of c is 6.

Question 5 :

w = 240 + 1.2 d

The weight of a flask containing a solution can be modeled by the equation above, where w is the weight in grams and d is the number of drops of solution that are in the flask. What is d when w is 300?

A) 50      B) 120     C) 276      D) 600

Solution :

When w = 300

300 = 240 + 1.2 d

300 - 240 = 1.2d

1.2d = 60

d = 60/1.2

d = 50

Question 6 :

Sunjay is traveling to a national park. The number of miles he needs to travel can be represented by the equation

M = 172 − 57h

where M is the the number of miles to the national park and h is the number of hours Sunjay has to travel. What is the meaning of the value 57 in this equation?

A) Sunjay started at a distance 57 miles from the national park.

B) Sunjay will reach the national park in 57 hours.

C) Sunjay travels to the national park at a rate of 57 miles per hour.

D) Sunjay has traveled 172 miles in 57 hours.

Solution :

Here  the rate of change is 57. So, option C is correct.

Question 7 :

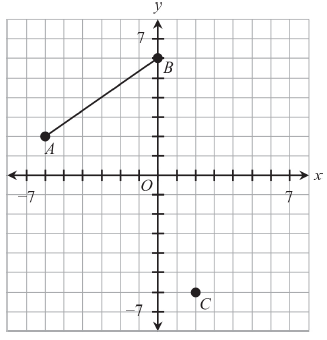
What is the equation of the line connecting the midpoint of line segment AB with point C in the figure above?

A) y = −2x − 2     B) y = −2x + 5    C) y = (2/3) x + 6

D) y = 2x − 2

Solution :

The line passes through the point A and B will be parallel to the line passes through the point C.

A(-6, 2) and B(0, 6)

Slope of the line AB = (6 - 2) / (0 + 6)

= 4/6

= 2/3

Slope of the line which passes through C is 2/3.

Equation of the line passes through the point C is 

(y - y₁) = m(x - x₁)

(y - 2) = (2/3)(x + 6)

y = (2/3)x + (2/3)(6) + 2

y = (2/3)x + 4 + 2

y = (2/3)x + 6

Question 8 :

Line y = mx + 5 passes through point (a, b), where a ≠ 0 and b ≠ 0. If m is a constant, what is the slope of the line in terms of a and b?

A)  (b - 5)/a     B)  (a - 5)/b      C)  (5 - b)/a

D)  (5 - a)/b

Solution :

The line y = mx + 5 passes through the point (a, b)

b = ma + 5

Solving for m, we get

b - 5 = ma

m = (b -5)/a

So, option A is correct.

Question 9 :

Julius has budgeted $150 per month for electricity. Last
month his electricity bill was $190 based on a rate of $0.12 per kilowatt hour. Which of the equations below represents the number of kilowatt hours, k, by which Julius needs to reduce his electricity usage this month in order to meet his budget?

A) k/0.12 = 40    B) k/12 = 40    C) 0.12k = 40

D) 0.12k = 150

Solution :

Last month bill = 190

Rate of change per kilowatt hour = 0.12

Her budget = 150

Electricity usage = 150/0.12

0.12k = 150

So, option D is correct.

Question 10 :

The line with the equation (2/3) x − (7/8) y = 2 is graphed in the xy-plane. What is the x-coordinate of the x-intercept of the line?

Solution :

(2/3) x − (7/8) y = 2

To find x-intercept, we apply y = 0

(2/3) x − 0 = 2

(2/3) x = 2

x = 2(3/2)

x = 3

So, x-intercept of the line is (3, 0).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.