AREA AROUND CIRCLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The area of a circle is the space occupied by the circle in a two-dimensional plane.
The formula for the area of a circle is
A = πr2
where r is the radius of the circle.
The value of pie is 22/7 or 3.14.
Example 1 :
Find the area of a ring whose outer radius is 20 cm and inner radius is 15 cm respectively.
Solution :
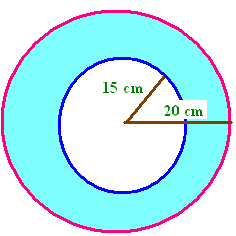
Let "R" be the radius of the outer circle.
Ler "r" be the radius of the inner circle.
Area of outer circle = ΠR²
Area of outer circle = Πr²
Radius of outer circle (R) = 20 cm
Radius of the inner circle (r) = 15 cm
Area of ring (shaded portion)
= Area of outer circle - area of inner circle
= ΠR² - Πr²
= Π (R² - r²)
= Π (20² - 15²)
= Π x (400 - 225)
= Π x 175
= (22/7) x 175
= 22 x 25
= 550 cm²
Example 2 :
There is an outside circular path had constructed around a circular garden. If the outer and inner circumferences of the path are 88 cm and 44 cm respectively. Find the width and area of the path.
Solution :
Circumference of outer circle = 88
2ΠR = 88
2 x (22/7) x R = 88
R = (88 x 7) /(2 x 22)
R = 2 x 7
R = 14 cm
Circumference of inner circle = 44
2Πr = 44
2 x (22/7) x r = 44
R = (44 x 7) /(2 x 22)
R = (2 x 7)/2
R = 7 cm
Width of path = R - r
= 14 - 7
= 7 cm
Area of outer path = ΠR²
= (22/7) x 14²
= (22/7) x 14 x 14
= 616 cm²
Area of inner path = Πr²
= (22/7) x 7²
= (22/7) x 7 x 7
= 154 cm²
Area of path = 616 - 154
= 462 cm²
Example 3 :
Find the area of the shaded region if radius of two concentric circles are 7cm and 14 cm respectively and ∠𝐴𝑂𝐶 = 40°.
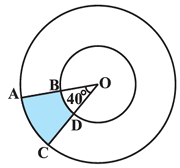
Solution :
Area of circle shaded = (θ/360) x ΠR² - (θ/360) x Πr²
= (θ/360)Π[R² - r²]
Here R = 14 cm and r = 7 cm
= (40/360)Π[14² - 7²]
= (1/9) x (22/7)[196 - 49]
= (22/9 x 7) x (147)
= (22 x 7/3)
= 154/3
= 51.33 cm2
Example 4 :
A race track is in the form of ring whose outer and inner circumferences are 506 m, 440 m respectively. Find the width of the track.
Solution :
Circumference of large circle = 506 m
2ΠR = 506 m
2 x 22/7 x R = 506
R = 506 x (7/22) x (1/2)
R = 506 x (7/22) x (1/2)
R = 161/2
= 80.5 cm
2Πr = 440 m
r = 440 x (7/22) x (1/2)
r = 440 x (7/22) x (1/2)
r = 70 cm
Radius of large circle = 80.5 cm
Radius of small circle = 70 cm
Area of width in between two circles = ΠR² - Πr²
= Π(R² - r²)
= 3.14(80.52 - 702)
= 3.14 (6480.25 - 4900)
= 3.14(1580.25)
= 4961.985 cm2
Example 5 :
In the given figure, AB is the diameter where AP = 12 cm and PB = 16 cm. If the value of p is taken 3, what is the perimeter of the shaded region?
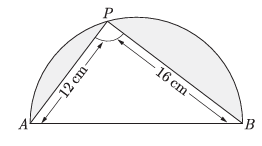
Solution :
AB is the diameter of the circle and APB is right triangle.
AB2 = AP2 + PB2
AB2 = 122 + 162
= 144 + 256
= √400
AB = 20 cm
Radius of circle = 10 cm
= (1/2) Πr² - (1/2) x base x height
= 1/2 [Πr² - 16 x 12]
= 1/2 [3.14 x 10² - 16 x 12]
= (1/2) [314 - 192]
= (1/2) x 122
= 61 cm2
Example 6 :
In given fig., O is the center of a circle. If the area of the sector OAPB is 5/36 times the area of the circle, what is the value of x?
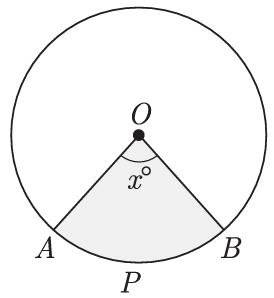
Solution :
Area of shaded region = 5/36 x area of circle
(θ/360) x Πr² = 5/36 x Πr²
θ/360 = 5/36
θ = (5/36) x 360
θ = 5 x 10
θ = 50
So, the required angle measure is 50 degree.
Example 7 :
In given figure arcs are drawn by taking vertices , AB and C of an equilateral triangle of side 10 cm, to intersect the side BC , CA and AB at their respective mid-points , DE and F. What is the area of the shaded region? (Use Π = . 3.14 )
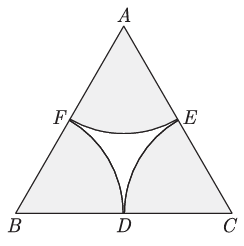
Solution :
Area of shaded region = 3 x (θ/360) x Πr²
Length of AB = 10 cm, since F is the midpoint AF = 5 cm
= 3 x (60/360) x Π(5)²
= 39.25 cm2
Related Pages
- Perimeter of sector
- practice questions with solution
- Length of arc
- Practice questions on length of arc
- Perimeter of square
- Perimeter of parallelogram
- Perimeter of rectangle
- Perimeter of triangle
- Area of a circle
- Area of Semicircle
- Area of Quadrant
- Area of sector
- Area of triangle
- Area of equilateral triangle
- Area of scalene triangle
- Area of square
- Area of rectangle
- Area of parallelogram
- Area of rhombus
- Area of trapezium
- Area of quadrilateral
- Area of pathways
- Area of combined shapes
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 43)
Jan 04, 26 01:38 AM
10 Hard SAT Math Questions (Part - 43) -
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations
