PERIMETER OF A TRIANGLE

Perimeter is a path that surrounds a two dimensional shape. The term may be used either for the path or its length it can be thought of as the length of the outline of a shape. 

Let a, b and c be the side lengths of a triangle. 

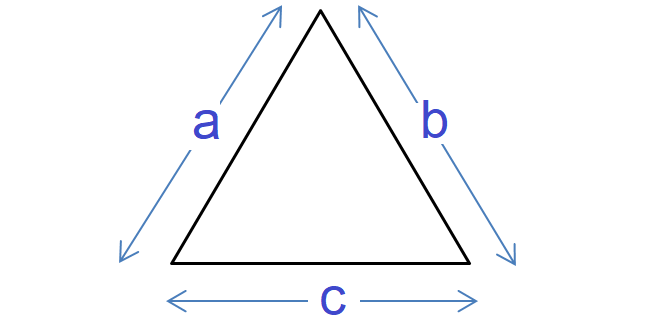
Perimeter of Triangle  =  a + b + c

Example 1 : 

Find the perimeter of the triangle shown below. 

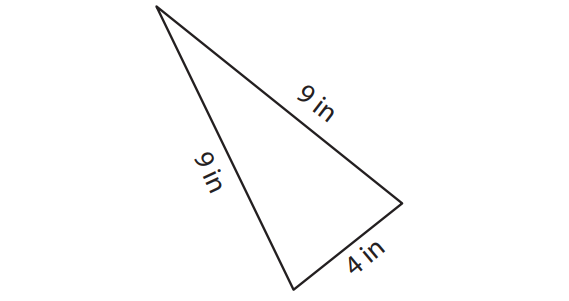
Solution :

Perimeter of the triangle :

=  9 + 9 + 4

=  22 in

Example 2 :

The sides of a triangle are 12 cm, 6 cm and 8 cm. Find the perimeter of the triangle.

Solution : 

Perimeter of the triangle : 

=  12 + 6 + 8

=  26 cm

Example 3 :

The length of each of side of an equilateral triangle is 7 in. Find the perimeter of the triangle.   

Solution :

Perimeter of the triangle :

=  7 + 7 + 7

=  21 in

Example 4 :

The length of each of the equal sides of an isosceles triangle is 3 cm and the length of the third side is 5 cm. Find the perimeter of the triangle.  

Solution :

Perimeter of the triangle :

=  3 + 3 + 5

=  11 cm

Example 5 :

The sides of a triangle are 2x, 3x and 4x. If the perimeter of the triangle is 81 in, then find the length of each side of the triangle. 

Solution :

Perimeter of the triangle  =  81 in

2x + 3x + 4x  =  81

9x  =  81

Divide each side by 9.

x  =  9

2x  =  2(9)  =  18

3x  =  3(9)  =  27

4x  =  4(9)  =  36

The lengths of the sides of the triangle are 18in, 27 in and 36 in. 

Example 6 :

If the perimeter of the triangle shown below is 101 cm, find the value of x. 

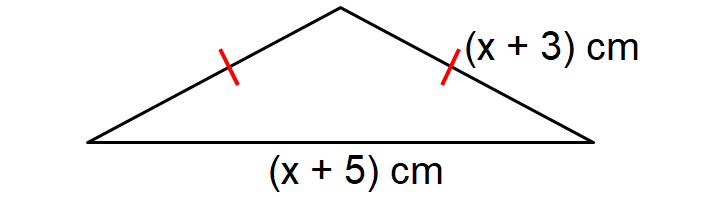
Solution :

The above triangle is an isosceles triangle and the length of each of the two equal sides is (x + 3) cm. 

Perimeter of the triangle  =  101 cm

(x + 3) + (x + 3) + (x + 5)  =  101

x + 3 + x + 3 + x + 5  =  101

3x + 8  =  101

Subtract 8 from each side. 

3x  =  93

Divide each side by 3. 

x  =  31

Example 7 :

The length of each of the equal sides of an isosceles triangle is 4 cm longer than the base. If the perimeter of the triangle is 62 cm, find the length of the sides of the triangles.

Solution :

Let x be the length of each of the two equal sides and y be the length of the base.

Then, x = y + 4. 

Perimeter of the triangle  =  62 cm

x + x + y  =  62

2x + y  =  62

Substitute x = y + 4. 

2(y + 4) + y  =  62

2y + 8 + y  =  62

3y + 8  =  62

Subtract 8 from each side. 

3y  =  54

Divide each side by 3. 

y  =  18

x  =  18 + 4

=  22

The length of the sides of the triangle are 22 cm, 22 cm and 18 cm.  

Example 8 :

Find the perimeter of the triangle defined by the following points : 

D(1, 3), E(8, 3) and F(4, 7)

Solution : 

Plot the points in the coordinate plane. Draw the height from F to the side DE. Label the point where the height meets DE as G. Point G has coordinates (4, 3). 

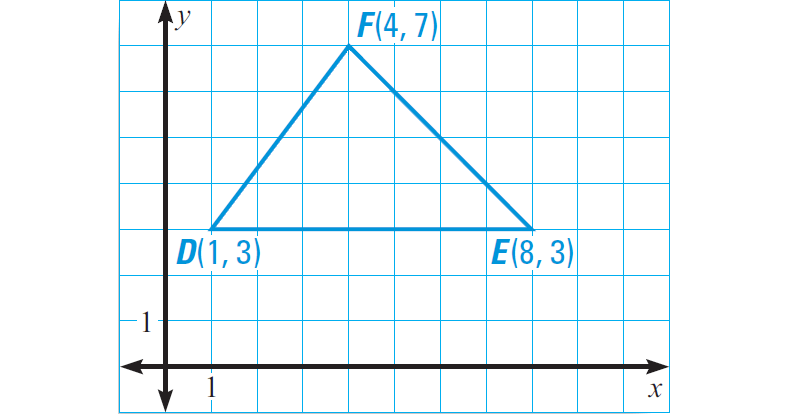
Length of DE : 

=  8 - 1

=  7

Use distance formula to find the length of EF and FD.

Distance Formula :

=  √[(x₂ - x₁)² + (y₂ - y₁)²]

Length of EF : 

(x₁, y₁)  =  E(8, 3)

(x₂, y₂)  =  F(4, 7)

EF  =  √[(4 - 8)² + (7 - 3)²]

EF  =  √[(-4)² + (4)²]

EF  =  √[16 + 16]

EF  =  √32

EF  =  √(4 ⋅ 4 ⋅ 2)

EF  =  4√2

Length of FD : 

(x₁, y₁)  =  F(4, 7)

(x₂, y₂)  =  D(1, 3)

FD  =  √[(1 - 4)² + (3 - 7)²]

FD  =  √[(-3)² + (-4)²]

FD  =  √[9 + 16]

FD  =  √25

FD  =  5

Perimeter of the triangle :

=  5 + 7 + 4√2

=  (12 + 4√2) units

Example 9 :

Area of a right triangle is 54 cm². If one of its legs is 12 cm long, its perimeter is

(a) 18 cm    (b) 27 cm    (c) 36 cm    (d) 54 cm

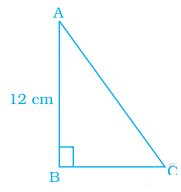
Solution :

Area of triangle = 54 cm²

height = 12 cm and base = ?

1/2 x base x 12 = 54

base x 6 = 54

base = 54/6

= 9

To find the perimeter, we have to find the hypotenuse.

AC² = AB² + BC²

AC² = 12² + 9²

= 144 + 81

AC² = 225

AC = 15 cm

Perimeter of the triangle = AB + BC + CA

= 12 + 9 + 15

= 36 cm

So, option c is correct.

Example 10 :

Area of an isosceles triangle is 48 cm². If the altitudes corresponding to the base of the triangle is 8 cm, find the perimeter of the triangle.

Solution :

Area of an isosceles triangle = 48 cm²

Let the equal sides be x.

1/2 x base x height = 48 cm²

1/2 x 8 x height = 48

height = 48/4

= 12 cm

4² + 12² = x²

16 + 144 = x²

160 = x²

x = 12.6 cm

Perimeter of triangle = 2x + 8

= 2(12.6) + 8

= 25.2 + 8

= 33.2 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.