AREA OF PARALLELOGRAM

A parallelogram is a quadrilateral in which opposite sides are parallel and equal in length.

In other words opposite sides of a quadrilateral are equal in length, then the quadrilateral is called a parallelogram.

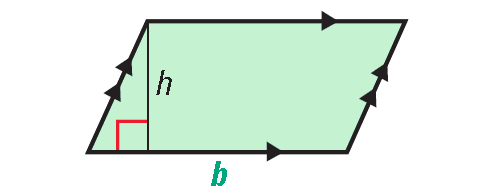
The area of a parallelogram is the product of a base and  its corresponding height.

Then, the formula to find area of a parallelogram is given by

A  =  b ⋅ h square units

We can justify the area for parallelogram as follows. 

The area of a parallelogram is the area of a rectangle with the same base and height. 

Examples

Example 1 : 

Find the area of the parallelogram ABCD shown below. 

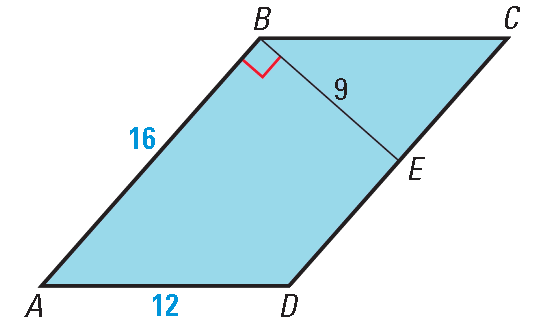
Solution :

Method 1 : 

Use AB as the base.

So, b  =  16 and h  =  9.

Formula for area of a parallelogram is 

=  b ⋅ h

Substitute the given measures. 

=  16 ⋅ 9

=  144 square units

Method 2 : 

Use AD as the base.

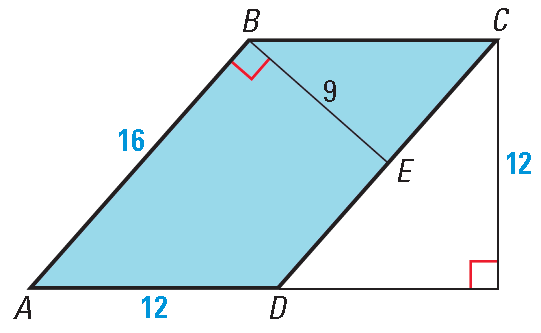
So, b  =  12 and h  =  12.

Formula for area of a parallelogram is 

=  b ⋅ h

Substitute the given measures. 

=  12 ⋅ 12

=  144 square units

Example 2 : 

Find the area of the parallelogram ABCD shown below. 

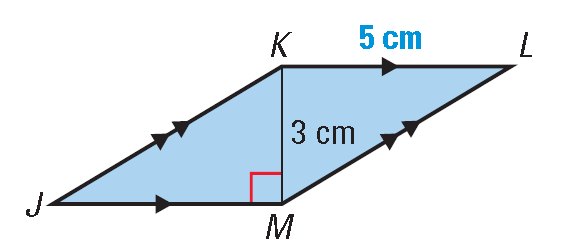
Formula for area of a parallelogram is 

=  b ⋅ h

Substitute b  =  5 and h  =  3.

=  5 ⋅ 3

=  15 square units

Example 3 :

A mirror is made of two congruent parallelograms as shown in the diagram. The parallelograms have a combined area of 9 1/3 square yards. The height of each parallelogram is 1 1/3 yards. How long is the base of each parallelogram ?

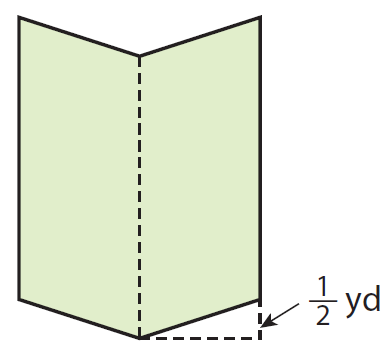
Solution :

Because the given parallelograms are congruent area of two parallelogram will be equal. 

Combined area of parallelograms  =  9 1/3 square yards

Combined area of parallelograms  =  28/3 square yards

Area of one parallelogram  =  (28/3) ÷ 2

Area of one parallelogram  =  14/3

b ⋅ h  =  14/3

b ⋅ 1 1/3  =  14/3

b ⋅ 4/3  =  14/3

Multiply each side by 3/4.

b  =  14/3 ⋅ 3/4

b  =  14/4

b  =  7/2

b  =  3 1/2

So, the base of the parallelogram is 3 1/2 yards.

Example 4 :

Find the base of a parallelogram if its area is 40 square cm and its altitude is 15 cm.

Solution :

Area of a parallelogram  =  40 cm²

b ⋅ h  =  40

Here, altitude (or) height (h)  =  15 cm.

b ⋅ 15  =  40

Divide each side by 15.

b  =  2.67

So, the base of the parallelogram is 2.67 inches. 

Example 5 :

Find the area of the shape shown below. 

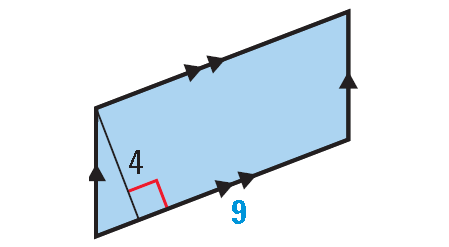
The above shape has four sides. So, it is a quadrilateral. Because the opposite sides are parallel, the above quadrilateral is a parallelogram. 

Formula for area of a parallelogram is 

=  b ⋅ h

Substitute b  =  9 and h  =  4.

=  9 ⋅ 4

=  36 square units

Example 6 :

If the area of the shape shown below is 60 square inches, then find the value of x. 

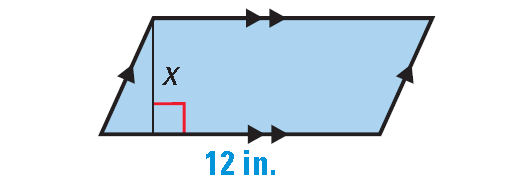
Solution :

Given : Area of the above shape is 60 square inches.  

The above shape has four sides. So, it is a quadrilateral. Because the opposite sides are parallel, the above quadrilateral is a parallelogram. 

Area  =  60 in²

b ⋅ h  =  60  

Substitute b  =  12 and h  =  x.

12 ⋅ x  =  60

Divide each side by 12.

x  =  5

Example 7 :

You make a photo prop for a school fair. You cut a 10-inch square out of a parallelogram-shaped piece of wood. What is the area of the photo prop?

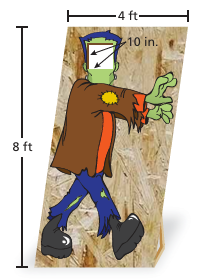
Solution :

Convert the dimensions of the piece of wood to inches.

12 inches = 1 foot

Base = 4 ⋅ 12

= 48 inches

Height = 8 ⋅ 12

= 96 inches

= area of wood − area of square

= 96(48) − 102

= 4608 − 100

= 4508

Example 8 :

The area of a parallelogram can be expressed as the binomial 2x² − 10x. Which of the following could be the length of the base and the height of the parallelogram?

a. 2x(x² − 5x)             b. 2x(x − 5) 

c. (2x − 1)(x − 10)           d. (2x − 5)(x + 2)

Solution :

Area of parallelogram = 2x² − 10x

Factoring 2x, we get

= 2x(x - 5)

Example 9 :

The perimeter of the parallelogram below is 32 cm. What is the length of the longer side?

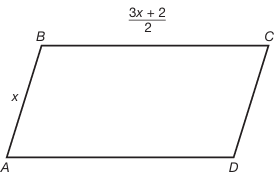
a. 9 cm      b. 10 cm      c. 6 cm     d. 12 cm

Solution :

Perimeter of parallelogram = 32 cm

Sum of all sides = 32

x + (3x + 2)/2 + x + (3x + 2)/2 = 32

2x + (6x + 4) /2 = 32

[4x + (6x + 4)]/2 = 32

10x + 4 = 32(2)

10x + 4 = 64

10x = 64 - 4

10x = 60

x = 60/10

x = 6

So, the value of x is 6. Option c is correct.

Example 10 :

Find the area of the shaded region. You cut a 12-inch square out of the piece of wood. What is the area of the photo prop?

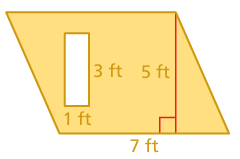
Solution :

Area of shaded region = area of parallelogram - area of rectangle

= (7 x 5) - (1 x 3)

= 35 - 3

= 32 square feet.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.