AREA OF TRAPEZIUM

Definition of Trapezium :

The definition of trapezium is entirely different in both US and UK.

• In US, a quadrilateral which is having no parallel sides is called trapezium.
• But in UK, a quadrilateral which is having one pair of parallel sides is called trapezium.

Definition of Trapezoid :

• In UK, a quadrilateral which is having no parallel sides is called trapezoid.
• But in US, a quadrilateral which is having one pair of parallel sides is called trapezoid.

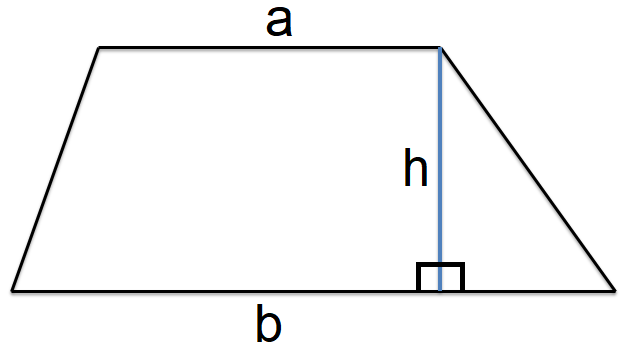
In the trapezium / trapezoid above, 'a' and 'b' are the lengths of the parallel sides and 'h' is the height.

Formula to Find Area of Trapezium / Trapezoid :

A  =  (1/2)(a + b)h

Examples

Example 1 :

Find the area of the trapezium ABCD shown below. 

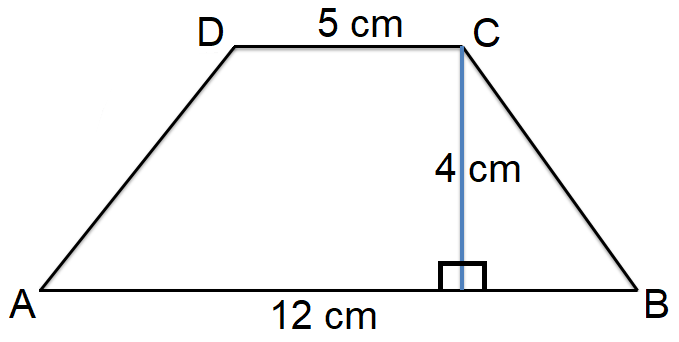
Solution :

Area of trapezium  =  (1/2)(a + b)h

Substitute a  =  5, b  =  12 and h  =  4.

=  (1/2)(5 + 12)4

=   (1/2)(17)4

=  34 cm² 

Example 2 :

In a trapezium the measurement of one parallel side two more than the other parallel side and the height is 4 cm. The area of the trapezium is 64 cm². Find the lengths of the two parallel sides.

Solution :

Let 'a' and 'b' be the two parallel sides.

One parallel side is two more than the other parallel side.

Then, 

a  =  b + 2

Area of the trapezium  =  64 cm²

(1/2)(a + b)h  =  64

Substitute h  =  4 and a  =  b + 2. 

(1/2)(b + 2 + a)4 = 64

(2b + 2)2  =  64

Divide each side by 2. 

2b + 2  =  32

Subtract 2 from each side. 

2b  =  30

Divide each side by 2. 

b  =  15

Then, 

a  =  b + 2

a  =  15 + 2

a  =  17

So, the lengths of the two parallel sides are 15 cm and 17 cm.

Example 3 :

The shape of the top surface of a table is a trapezium. Find its area, if its parallel sides are 1 m and 1.2 m and perpendicular distance between 0.8 m.

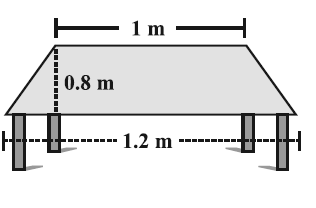
Solution :

Area of a the top of surface of the table (trapezium) is

=  (1/2)(a + b)h

=  (1/2)(1.2 + 1)0.8 

=  (1/2) (2.2)0.8 

=  1.1 (0.8)

=  8.8 m²

Example 4 :

The wall is in the shape as shown below has to be painted. If one can of paint covers 0.5 m², how many cans of paint will be needed, if only one coat of paint is applied ?

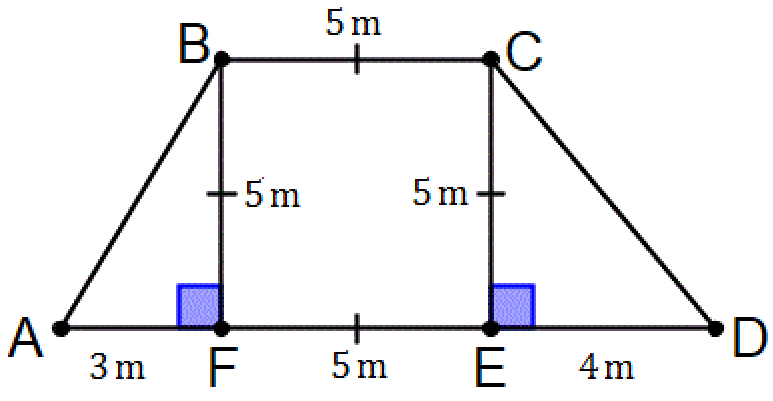
Solution :

In the figure shown above, the perpendicular distance between the two sides BC and AB at any point is same, which is 5 cm. 

Then, the sides BC and AD are parallel. 

In the quadrilateral above, because the two sides BC and AD are parallel, ABCD is a trapezium. 

Let 'a' and 'b' be the lengths of two parallel sides and. 

a  =  BC  =  5cm

b  =  AD  =  AF + FE + ED  =  3 + 5 + 4  =  12 cm

Height (h)  =  5 cm  

Area of the trapezium ABCD is 

=   (1/2)(a + b)h

Substitute a  =  5, b  =  12 and h  =  5.

=  (1/2)(5 + 12)5

=  42.5 m²

One can of paint covers 0.5 m².

Number of cans of paint required 42.5 m² is

=  42.5 / 0.5

=  425 / 5

=  85

So, 85 cans of paint required to cover the above wall. 

Example 4 :

The two parallel sides of a trapezium are 1.5 m and 2.5 m respectively. If the perpendicular distance between them is 6.5 meters, the area of the trapezium is :

a)  10 m²    b)  13 m²     c)  20 m²       d) 26 m²

Solution :

Length of parallel sides, a = 1.5 m and b = 2.5 m

height = 6.5 m

Area of trapezium = (1/2)(a + b)h

= (1/2) x 6.5 (1.5 + 2.5)

= (1/2) x 6.5 x 4

= 2 x 6.5

= 13 m²

So, option b is correct.

Example 5 :

The area of the field in the shape of trapezium measures 1440 m². The perpendicular distance between its parallel sides is 24 m. If the ratio of the parallel sides is 5 : 3 the length of the longer parallel side is :

a)  45 m    b)  60 m     c)  75 m       d) 120 m

Solution :

Area of trapezium = 1440 m²

height = 24 m

Let 5x and 3x be the length of parallel sides.

(1/2)(a + b)h = 1440

(1/2)(5x + 3x)24 = 1440

12(8x) = 1440

x = 1440/12 x 8)

x = 15

3x = 3(15) ==> 45 m

5x = 5(15) ==> 75 m

So, the length of longer parallel side is 75 m.

Example 6 :

The cross section of a canal is trapezium in shape. The canal is 12 m wide at the top and 8 m wide at the bottom. If the area of the cross The area of the cross section is 840 sq.cm the depth of the canal is :

a)  8.75 m    b)  42 m    c)  63 m    d)  84 m

Solution :

Length of parallel sides, a = 12 m, b = 8 m

Area of the cross section = 840 sq.cm

Let h be the depth of trapezium.

(1/2) h (12 + 8) = 840

(1/2) x h(20) = 840

10h = 840

h = 840/10

h = 84 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.