PERIMETER OF SQUARE

A square is a four-sided closed figure where the lengths of all the four sides will be equal and each vertex angle will be right angle or 90^o as shown below. 

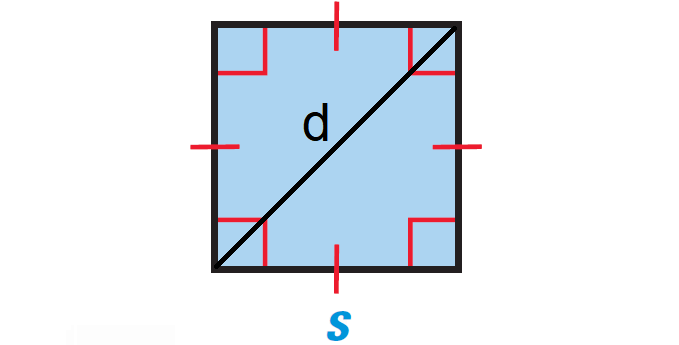
Formula for Perimeter of Square

Let s be the length of each side of a square. 

Then, 

Perimeter  =  4s

Examples

Example 1 :

Find the perimeter of the square having side length 14 cm.

Solution :

Formula for perimeter of a square :

=  4s 

Substitute 14 for s.

=  4(14)

=  56

So, the perimeter of the square is 56 cm.

Example 2 :

If the perimeter of square is 32 inches, then find the length of each side. 

Solution :

Perimeter of the square  =  32 inches

4s  =  32

Divide each side by 4.

 s  =  8 

So, the length of each side of the square is 8 inches. 

Example 3 :

The square has side length 250 cm. Find its perimeter in meter.

Solution :

Formula for perimeter of a square :

=  4s 

Substitute 250 for s.

=  4(250)

=  1000 cm -----(1)

We know  

100 cm  =  1 m

Therefore, to convert centimeter to meter,  we have to divide by 100. 

(1)-----> Perimeter  =  1000 cm

Divide the right side by 100 to convert cm into m.

Perimeter  =  (1000 / 100) m

=  10 m

So, the perimeter of the square is 10 meters.

Example 4 :

If the length of each diagonal of a square is 2√2 cm, then find its perimeter.

Solution :

To find the perimeter of a square, first we have to know the length of each side.

Let s be the length of each side of the square. 

Draw a sketch. 

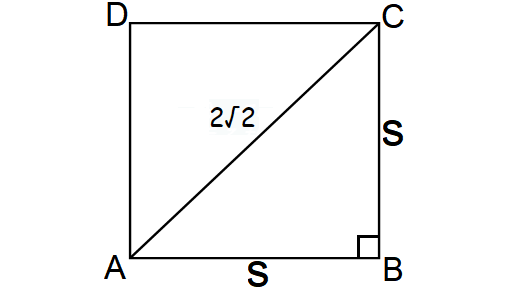
In the figure shown above, consider the right triangle ABC. 

By Pythagorean Theorem, we have

AB² + BC²  =  AC²

Substitute.

s² + s²  =  (2√2)²

Simplify and solve for s. 

2s²  =  2² ⋅(√2)²

2s²  =  4 ⋅(2)

2s²  =  8

Divide each side by 2. 

s²  =  4

Find positive square root on both sides.

 √s²  =  √4

 √s²  =  √(2 ⋅ 2)

s  =  2

Formula for perimeter of a square. 

Perimeter  =  4s

Substitute 2 for s. 

=  4(2)

=  8

So, the perimeter of the square is 8 cm. 

Example 5 :

If the lengths of the sides of two squares are in the ratio 2 : 5. then find the ratio of their perimeters.

Solution :

From the ratio 2 : 5, let the sides  of two squares be 2x and 5x respectively.

Formula for perimeter of a square :

=  4s

Ratio of the perimeters :

=  8x : 10x

Divide each term by 2x.

=  2 : 5

So, the ratio of the perimeters of two squares is 2 : 5.

Note :

The ratio of the sides of two squares and the ratio of the perimeters of two squares are same. 

Apart from the stuff given in this section,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and Venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6