AREA OF EQUILATERAL TRIANGLE

What is equilateral triangle ?

In geometry, an equilateral triangle is a triangle in which all three sides are equal. The area enclosed by this shape is known as area of equilateral triangle.

Area of equilateral triangle can be found using the formula given below.

Area of Equilateral Triangle  =  (√3/4)a² sq. units

where a is the length of each side of the triangle. 

Deriving the Formula to Find the Area of Equilateral Triangle

Take an equilateral triangle of the side “a” units. Then draw a perpendicular bisector to the base of height “h”.

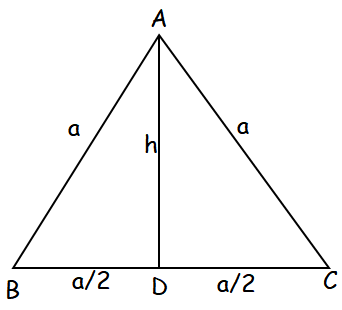
By drawing perpendicular from A, we get two congurent right triangle ABD and ADC.

Area of triangle ABC  =  Area of triangle ABD + Area of triangle ADC

Since triangles ABD and ADC are congurent, areas will be equal.

Area of triangle ABC  =  Area of ABD + Area of ADC

Area of triangle ABC  =  2  (Area of ABD)

=  2 ⋅ (1/2) ⋅ Base ⋅ Height

Area of triangle ABC  =  Base ⋅ Height  ---(1)

In triangle ABD,

Base (BD)  =  a/2 and height (AD)  =  h

Using Pythagorean theorem,

a²  =  h² + (a/2)²

h²  =  a² - (a²/4)

h²  =  (3a²/4)

h  =  √(3a²/4)

h  =  (a√3/2)

By applying the values of base and height in (1), we get

Area of triangle ABC  =  (a/2) ⋅ (a√3/2)

  =  (1/4)a²√3

Area of triangle ABC  =  √3a²/4 square units

Examples

Example 1 :

Find the area of the equilateral triangle having the length of the side equals 10 cm.

Solution :

Area of equilateral triangle  =  (√3/4) a²

Here a = 10 cm

  =  (√3/4) (10)²

  =  (√3/4) x (10) x (10)

  =  (√3) x (5) x (5)

  =  25 √3 cm²

Example 2 :

Find the length of the altitude of an equilateral triangle of side 3√3 cm.

Solution :

Side length of equilateral triangle (a)  =  3√3

Area of equilateral triangle  =  (√3/4) a²

  =  (√3/4) (3√3)²

=  (√3/4) (27)

Area of equilateral triangle  =  27√3 / 4   ---(1)

Here we should find the length of altitude,  so we use the formula base ⋅ height to find the area of equilateral triangle.

=   base ⋅ height

  =  (3√3/2) ⋅ h    ------(2)

(1)  =  (2)

(3√3/2) ⋅ h  =  27√3/4

h  =  (27√3/4) ⋅ (2/3√3)

h  =  9/2 

h  =  4.5

So, the required height is 4.5 cm.

After having gone through the stuff given above, we hope that the students would have understood how we derive the formula for area of equilateral triangle and examples.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and Venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6