PROBLEMS ON AREA AND PERIMETER OF COMBINED FIGURES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
Find the perimeter and area of the following figures:
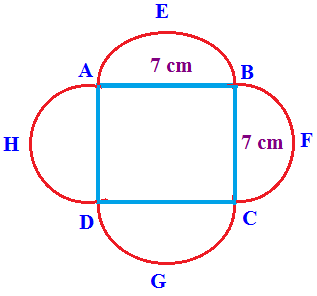
Solution :
In the above figure we have four semi circles and one square. To find the perimeter, we have to add the sum of four semicircles and a square.
Radius = 7/2 => 3.5 cm
Length of each side of square = 7 cm
The perimeter of the given figure
= 4 (perimeter of semicircles) + Perimeter of square
Perimeter of semi circle AEB = Π r
= (22/7) x 3.5
= 22 x 0.5
= 11
Perimeter of 4 semi circles = 4 (11)
= 44 cm
Perimeter of square = 4a
= 28 cm
The perimeter of the given figure = 44 cm + 28 cm
= 72 cm
Area of 1 semi circle = Π r²/2
= (1/2) x (22/7) x (7/2)2
= (1/2) x (22/7) x (7/2) x (7/2)
= (1/2) x 11 x (7/2)
= 77/4
= 19.25 cm²
Area of 4 semi circles = 4 (19.25)
= 77
Area of square = a2
= 7x7
= 49 cm2
Area of given figure
= Area of 4 semi circles + Area of square
= 77 + 49
= 126 cm2
Example 2 :
Find the area of shaded portion.
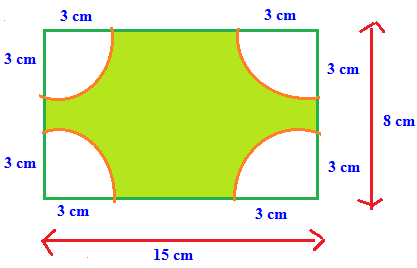
Solution :
Area of shaded portion
= Area of rectangle - Area of 4 quadrants of circle
Area of rectangle = Length x Width
Length of rectangle = 15 cm
Width of rectangle = 8 cm
= 15 x 8
= 120 cm²
Area of quadrant = Π r²/4
radius of quadrant = 3 cm
= [(22/7) x 3²]/4
= (22 x 3 x 3)/(7 x 4)
= 198/28
Area of 4 quadrant = 4 x 198/28
= 198/7
= 28.28 cm²
Area of shaded portion = 120 - 28.28
= 91.715 cm2
Example 3 :
The kitchen in Mario’s Italian restaurant is 18 meters long and 12 meters wide. A square pantry is connected to the kitchen area. The pantry is 3 meters wide. What is the total area of the kitchen and pantry?
Solution :
Total area of the kitchen and pantry = Area of rectangle + Area of square
Area of rectangle = length x width
Area of square = a x a
Length of rectangle = 18 m and width = 12 m
Side length square pantry = 3 m
Required area = (18 x 12) + (3 x 3)
= 216+9
= 225 square meter
Example 4 :
The area of triangle QTU is 6 square units, and the area of triangle RSU is 6 square units. The dimensions in the figure below are labeled in units. What is the area of triangle STU in square units?
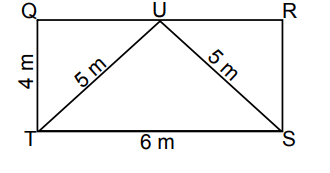
Solution :
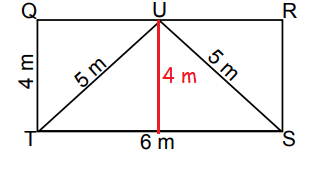
Area of triangle SUT
= Area of rectangle TQRS - 2(Area of TQU)
Area of rectangle = length x width
= 6 x 4
= 24 m2
TU2 = TQ2 + UQ2
52 = 42 + UQ2
UQ2 = 25-16
UQ2 = 9
UQ = 3
Area of triangle TQU = (1/2) x base x height
= (1/2) x 3 x 4
= 6
Area of triangles TQU and SRU = 12
Required area = 24 - 12
= 12 m2
Example 5 :
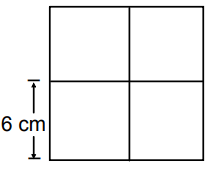
The figure below is divided into four small
squares. The sides of each small square are 6
cm long. What is the area, in square
centimeters, of the entire figure?
Solution :
Area of square = a x a
Side length = 6 + 6 ==> 12 cm
Area of square = 12 x 12
= 144 cm2
Example 6 :
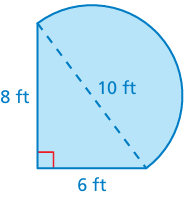
The figure is made up of a semicircle and a triangle. Find the perimeter
Solution :
Area of composite figure = area of triangle + area of semicircle
= (1/2) x base x height + (1/2) πr2
Base of triangle = 6 ft, height of triangle = 8 ft
radius of semicircle = 5 ft
= (1/2) x 6 x 8 + (1/2) π(5)2
= 24 + 0.5 x 3.14 x 25
= 24 + 39.25
= 63.25 square feet.
Example 7 :
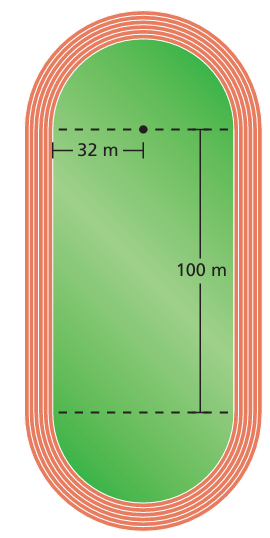
The running track is made up of a rectangle and two semicircles. Find the perimeter.
Solution :
Radius of semicircle = 32 m
length of rectangle = 100 m
= 2 πr + 2(length of rectangle)
= 2 x 3.14 x 32 + 2(100)
= 200.96 + 200
= 400.96 square meter
Example 8 :
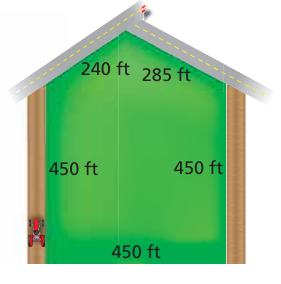
A section of land is to be fenced in for a horse pasture.
a. Find the perimeter of the pasture.
b. Fencing costs $27 per yard. How much will it cost to fence in the pasture?
Solution :
a) Perimeter of the pasture
= 450 + 450 + 450 + 240 + 285
= 3(450) + 240 + 285
= 1350 + 240 + 285
= 1875 ft
b) Fencing cost = $27 per yard
1 yard = 3 ft
1 ft = 1/3 yard
1875 ft = 1875/3 yards
= 625 yards
Required cost = 625 x 27
= $16875
Example 9 :
The inner circumference is 352 mm and outer is 396 mm. Find the width of circular design.

Solution :
Let r be the radius of smaller circle and R be the radius of larger circle.
Circumference of smaller circle = 2πr
Circumference of smaller circle = 2πR
|
2πR = 396 mm R = 396/2π = 63.05 |
2πr = 352 mm r = 352/2π = 56.05 |
Width = R - r
= 63.05 - 56.05
Width = 7 mm
So, width of the circular design is 7 mm.
Example 10 :
A rectangular field is 48 m long and 12 m wide. How many right triangular flower beds can be laid in this field, if sides including the right angle measure 2 m and 4 m, respectively?
Solution :
Area of rectangle = 48 x 12
= 576 square meter
Area of right triangle = (1/2) x 2 x 4
=4 square meter
Number of flower beds = 576/4
= 144 flower beds
Example 11 :
A design is made up of four congruent right triangles as shown in figure. Find the area of the shaded portion.
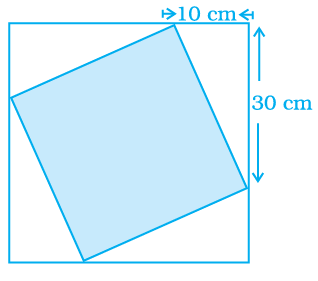
Solution :
At corners we have right triangle.
Length of hypotenuse = side length of square
l = √102 + 302
= √(100 + 900)
= √1000
= 10 √10
Area of square = (side)2
= (10 √10)2
= 100(10)
= 1000 square cm
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
