AREA AND PERIMETER OF QUADRANT
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Here we are going to see the how to find area and perimeter of quadrant.
A quadrant is exactly one fourth of any circle.
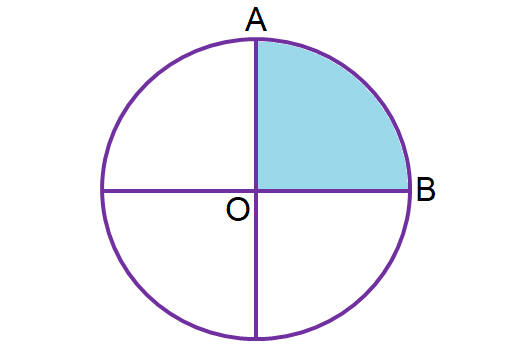
Area of a quadrant = (1/4)πr2
Perimeter of a quadrant = ((π/2) + 2)r
It has 90 degree angle at the center.
Example 1 :
Find the area of quadrant with radius 7 cm.
Solution :
Here r = 7 cm and π = 22/7.
= (1/4) ⋅ (22/7) ⋅ (7)2
= (1/4) ⋅ (22/7) ⋅ 7 ⋅ 7
= (1/4) ⋅ 22 ⋅ 7
= (1/2) ⋅ 11 ⋅ 7
= 11 ⋅ 3.5 = 38.5 cm2
Example 2 :
Find the area of quadrant with radius 3.5 cm.
Solution :
Here r = 3.5 cm and π = 22/7.
= (1/4) ⋅ (22/7) ⋅ (3.5)²
= (1/4) ⋅ (22/7) ⋅ 3.5 ⋅ 3.5
= (1/4) ⋅ 22 ⋅ 0.5 ⋅ 3.5
= (1/2) ⋅ 11 ⋅ 0.5 ⋅ 3.5
= 10.5 ⋅ 0.5 ⋅ 3.5
= 18.375 cm2
Example 3 :
Find the area of quadrant with radius 64 cm.
Solution :
Here r = 3.5 cm and π = 22/7.
= (1/4) x (22/7) x (64)2
= (1/4) x (22/7) x 64 x 64
= (22/7) x 16 x 64
= (22 x 16 x 64)/7
= 22528/7
= 3218.28 cm2
Example 4 :
Find the perimeter of the quadrant with radius 7 cm.
Solution :
Here r = 7 cm and π = 22/7.
Circumference of quadrant = [(Π/2) + 2]r
= [(22/14) + 2] (7)
= [(11/7) + 2] 7
= ((11 + 14)/7) 7
= 25 cm
Example 5 :
Find the perimeter of the quadrant with radius 4.2 cm.
Solution :
Here r = 4.2 cm and π = 22/7.
= [(22/14) + 2] (4.2)
= [(11/7) + 2] 4.2
= ((11 + 14)/7) 4.2
= (25/7) ⋅ 4.2
= 25(0.6)
= 15 cm
Example 6 :
Find the perimeter the quadrant with radius 14 cm.
Solution :
Here r = 14 cm and π = 22/7.
= [(22/14) + 2] (14)
= [(11/7) + 2] 14
= ((11 + 14)/7) 14
= (25/7) ⋅ 14
= 25(2)
= 50 cm
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 25)
Feb 28, 26 07:21 AM
Digital SAT Math Problems and Solutions (Part - 25) -
Digital SAT Math Problems and Solutions (Part - 21)
Feb 28, 26 06:49 AM
Digital SAT Math Problems and Solutions (Part - 21) -
Digital SAT Math Problems and Solutions (Part - 24)
Feb 28, 26 03:00 AM
Digital SAT Math Problems and Solutions (Part - 24)