TRIGONOMETRY WORD PROBLEMS WORKSHEET ANGLE OF ELEVATION AND DEPRESSION

(1)  A ramp for unloading a moving truck, has an angle of elevation of 30°. If the top of the ramp is 0.9 m above the ground level, then find the length of the ramp.

Solution

(2)  A girl of height 150 cm stands in front of a lamp-post and casts a shadow of length 150 √3 cm on the ground. Find the angle of elevation of the top of the lamp-post.

Solution

(3)  Suppose two insects A and B can hear each other up to a range of 2 m.. The insect A is on the ground 1 m away from a wall and sees her friend B on the wall, about to be eaten by a spider. If A sounds a warning to B and if the angle of elevation of B from A is 30°, will the spider have a meal or not ? ( Assume that B escapes if she hears A calling )                     Solution

(4) To find the cloud ceiling, one night an observer directed a spotlight vertically at the clouds. Using a theodolite placed 100 m from the spotlight and 1.5 m above the ground, he found the angle of elevation to be 60°. How high was the cloud ceiling? (Hint : See figure) 

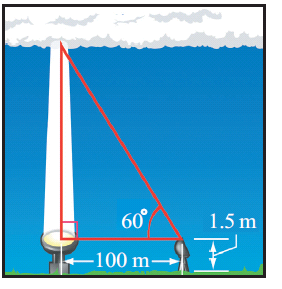
cloud is present. The cloud ceiling at airports must be
sufficiently high for safe take offs and landings. At night
the cloud ceiling can be determined by illuminating the base of the clouds by a spotlight pointing vertically upward.)                 Solution

(5)  A simple pendulum of length 40 cm subtends 60c at the vertex in one full oscillation. What will be the shortest distance between the initial position and the final position of the bob? (between the extreme ends)

Solution

(6)  Two crows A and B are sitting at a height of 15 m and 10 m in two different trees vertically opposite to each other . They view a bread (an eatable) on the ground at an angle of depression 45° and 60° respectively. They start at the same time and fly at the same speed along the shortest path to pick up the bread. Which bird will succeed in it? Hint : (foot of two trees and bread (an eatable) are in a straight line)                 Solution

(7)  A lamp-post stands at the centre of a circular park. Let P and Q be two points on the boundary such that PQ subtends an angle 90° at the foot of the lamp-post and the angle of elevation of the top of the lamp post from P is 30°. If PQ = 30 m, then find the height of the lamp post.                Solution

(8)  A person in an helicopter flying at a height of 700 m, observes two objects lying opposite to each other on either bank of a river. The angles of depression of the objects are 30° and 45°. Find the width of the river. ( √3 = 1.732 )                  Solution

(9)  A person X standing on a horizontal plane, observes a bird flying at a distance of 100 m from him at an angle of elevation of 30c. Another person Y standing on the roof of a 20 m high building, observes the bird at the same time at an angle of elevation of 45°. If X and Y are on the opposite sides of the bird, then find the distance of the bird from Y.               Solution

(10)  A student sitting in a classroom sees a picture on the black board at a height of 1.5 m from the horizontal level of sight. The angle of elevation of the picture is 30°. As the picture is not clear to him, he moves straight towards the black board and sees the picture at an angle of elevation of 45°. Find the distance moved by the student.

Solution

(11)  A boy is standing at some distance from a 30 m tall building and his eye level from the ground is 1.5 m. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

Solution

(12)  From the top of a lighthouse of height 200 feet, the lighthouse keeper observes a Yacht and a Barge along the same line of sight . The angles of depression for the Yacht and the Barge are 45° and 30° respectively. For safety purposes the two sea vessels should be at least 300 feet apart. If they are less than 300 feet , the keeper has to sound the alarm. Does the keeper have to sound the alarm ?               Solution

(13)  A boy standing on the ground, spots a balloon moving with the wind in a horizontal line at a constant height . The angle of elevation of the balloon from the boy at an instant is 60°. After 2 minutes, from the same point of observation,the angle of elevation reduces to 30c. If the speed of wind is 29 √3 m/min. then, find the height of the balloon from the ground level.             Solution

(14)  A straight highway leads to the foot of a tower . A man standing on the top of the tower spots a van at an angle of depression of 30 c. The van is approaching the tower with a uniform speed. After 6 minutes, the angle of depression of the van is found to be 60°. How many more minutes will it take for the van to reach the tower? 

Solution

(15)  The angles of elevation of an artificial earth satellite is measured from two earth stations, situated on the same side of the satellite, are found to be 30° and 60°. The two earth stations and the satellite are in the same vertical plane. If the distance between the earth stations is 4000 km, find the distance between the satellite and earth. ( √3 = 1.732)            Solution

(16)  From the top of a tower of height 60 m, the angles of depression of the top and the bottom of a building are observed to be 30° and 60° respectively. Find the height of the building.             Solution

(17)  From the top and foot of a 40 m high tower, the angles of elevation of the top of a lighthouse are found to be 30° and 60° respectively. Find the height of the lighthouse. Also find the distance of the top of the lighthouse from the foot of the tower.            Solution

(18)  The angle of elevation of a hovering helicopter as seen from a point 45 m above a lake is 30° and the angle of depression of its reflection in the lake, as seen from the same point and at the same time, is 60°. Find the distance of the helicopter from the surface of the lake. 

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.