ANGLE OF ELEVATION AND DEPRESSION EXAMPLES

Example 1 :

A student sitting in a classroom sees a picture on the black board at a height of 1.5 m from the horizontal level of sight. The angle of elevation of the picture is 30°. As the picture is not clear to him, he moves straight towards the black board and sees the picture at an angle of elevation of 45°. Find the distance moved by the student.

Solution :

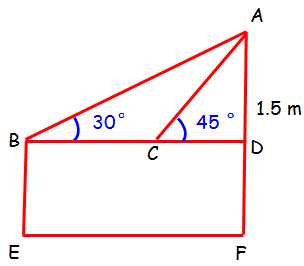
Distance moved by the student  =  BC

In triangle ABD :

∠ABD  =  30°

  tan θ = opposite side/Adjacent side

tan 30°  =  AD/BD

1/√3  =  1.5/BD

BD  =  1.5 x √3 ==> 1.5 √3

In triangle ACD :

∠ACD  =  45°

  tan θ = opposite side/Adjacent side

tan 45°  =  AD/CD

1  =  1.5/CD

CD  =  1.5

BC  =  BD - CD  

BC  =  1.5 √3 - 1.5

=  1.5 (√3 - 1) = 1.5(1.732 - 1)

=  1.5 (0.732) ==> 1.098 m

Hence the distance moved by the student is 1.098 m.

Example 2 :

A boy is standing at some distance from a 30 m tall building and his eye level from the ground is 1.5 m. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

Solution :

From the given information, we can draw a rough diagram 

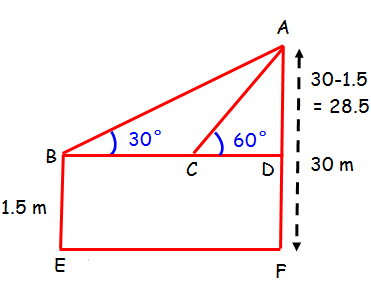
AD  =  28.5 m 

In triangle ABD

∠ABD  =  30°

  tan θ = opposite side/Adjacent side

  tan 30° = AD/BD

  1/√3  =  28.5/BD ==> BD  = 28.5 √3 --(1)

In triangle ACD

∠ABD  =  60°

  tan θ = opposite side/Adjacent side

  tan 60° = AD/CD

  √3  =  28.5/CD ==> CD  = 28.5/√3 

Multiplying by √3 on both numerator and denominator, we get

CD  =  28.5/√3 ==> 28.5√3/3  ==> 9.5√3  -->(2)

the distance he walked towards the building =  BD - CD 

  =  28.5 √3  -  9.5√3 ==> 19√3 m

Example 3 :

From the top of a lighthouse of height 200 feet, the lighthouse keeper observes a Yacht and a Barge along the same line of sight .The angles of depression for the Yacht and the Barge are 45° and 30°  respectively. For safety purposes the two sea vessels should be at least 300 feet apart. If they are less than 300 feet , the keeper has to sound the alarm. Does the keeper have to sound the alarm ?

Solution : 

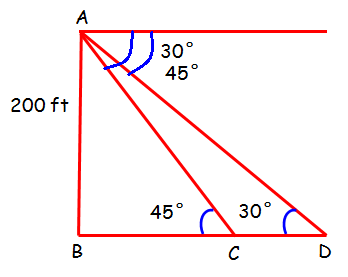
From the above picture, we have to find the value of CD.

In triangle ABC

∠ACB  =  45°

sin θ = opposite side/Hypotenuse side

sin 45°  =  AB/BC

1/√2  =  200/BC

BC  =  200 √2

In triangle ABD

∠ADB  =  30°

sin 30°  =  AB /BD

1/2  =  200/BD

BD = 200 x 2 ==> 400

CD = BD - BC ==> 400 - 200 √2 ==> 200(2 - √2)

  =  200 (2 - 1.414)

  =  200(0.586) ==> 117.2 m

From this, we come to know that the distance between  Yacht and a Barge is less than 300 m. Hence the keeper has to sound the alarm.

Example 4 :

A surveyor is standing 50 feet from the base of a large tree. The surveyor measures the angle of elevation to the top of the tree as 71.5°. How tall is the tree?

Solution : 

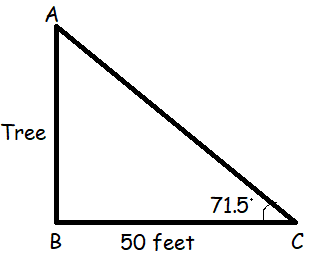
AB = opposite side, BC = adjacent side and AC = Hypotenuse

tan θ = Opposite side/Adjacent side

tan 71.5 = AB/BC

tan 71.5 = AB/50

AB = 50 tan 71.5

= 50(2.98)

AB = 149 ft

So, the height of the tree is 149 ft.

Example 5 :

At a point 200 feet from the base of a building, the angle of elevation to the bottom of a smokestack on the roof of the building is 35°, and the angle of elevation to the top of the smokestack is 53°. Find the height of the smokestack.

Solution : 

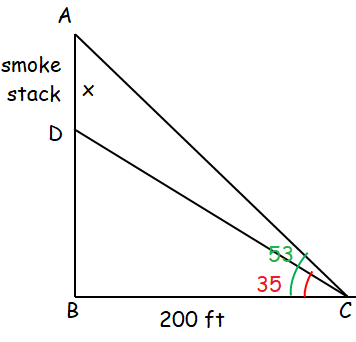
In triangle DBC,

tan θ = Opposite side/Adjacent side

tan 35 = DB/BC

tan 35 = DB/200

DB = 200(tan 35)

= 200 (0.700)

DB = 140

In triangle ABC,

tan 53 = (AD + DB)/BC

tan 53 = (140 + x)/200

140 + x = 200(tan 53)

140 + x = 200 (1.327)

140 + x = 265.4

x = 265.4 - 140

x = 125.4 ft

So, height of the smokestack is 125.4 ft.

Example 6 :

A kite is floating above a straight road. To estimate its height above the ground, the kite flyers simultaneously measure the angle of depression to two consecutive mileposts (meaning each post is a mile apart) on the road on the same side of the kite. The angles of depression are found to be 15° and 31°. How high is the kite?

Solution :

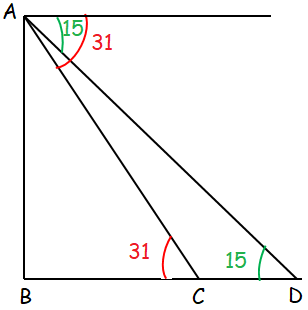
Opposite side = AB, BC and BD = adjacent sides and

AD = hypotenuse

In triangle ADB,

tan θ = Opposite side/Adjacent side

tan 15 = AB/BD

0.2679 = AB/BD

0.2679 = AB/(BC + CD)

AB = 0.2679(BC + CD) ------(1)

tan 31 = AB/BC

0.600 = AB/BC

AB = 0.6(BC) ------(2)

(1) = (2)

0.2679(BC + CD) = 0.6(BC)

CD = 1 (consecutive miles)

0.2679 BC - 0.6BC = -0.2679 CD

0.3321 BC = 0.2679

BC = 0.2679/0.3321

BC = 0.806 miles

1 mile = 5280 ft

0.806 miles = 0.806(5280)

= 4255.68 ft

Applying the value of BC,

AB = 0.6(0.806)

= 0.483 miles

0.483 miles = 0.483 (5280)

= 2550.24 ft

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.