WORD PROBLEMS INVOLVING ANGLE OF ELEVATION IN TRIGONOMETRY

Problem 1 :

A lamp-post stands at the centre of a circular park. Let P and Q be two points on the boundary such that PQ subtends an angle 90°  at the foot of the lamp-post and the angle of elevation of the top of the lamp post from P is 30° . If PQ = 30 m, then find the height of the lamp post.

Solution :

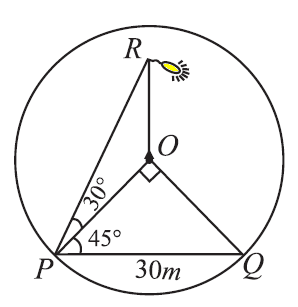
Let O be the centre of the park and OR be the lamp post. P and Q are two points on the boundary of the circular park. Given that PQ = 30m,

∠POQ  = 90°

In a right triangle OPQ, ∠POQ  = 90°

OP = OQ = radius. So ∠OPQ  = ∠OPQ  = 45°

OP = PQ x cos 45°

OP = 30/√2 ==> (30/√2) x (√2/√2) ==> 15 √2

In a triangle RPO  

tan 30° = OR/OP

1/√3 = OR/15√2

OR = (15√2/√3) ==> (15√2/√3) x (√3/√3)

  =   15√6/3 ==> 5√6

So, the height of the lamp post is 5√6 m.

Problem 2 :

A person in an helicopter flying at a height of 700 m, observes two objects lying opposite to each other on either bank of a river. The angles of depression of the objects are 30° and 45°. Find the width of the river. (√3 = 1.732 )

Solution :

From the given information, we can draw a rough diagram 

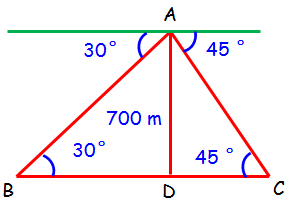
AD  =  700 m 

In triangle ACD, we need to find the length of DC.

∠ACD  =  45°

  tan θ = opposite side/Adjacent side

  tan 45° = AD/DC

  1  =  700/DC ==> DC  = 700  --(1)

In triangle ABD, we need to find the length of BD.

∠ABD  =  30°

  tan θ = opposite side/Adjacent side

  tan 30° = AD/BD

  1/√3  =  700/BD ==> BD  = 700√3  --(2)

(1) + (2) 

Width of the river  =  BD + DC  ==>  700 + 700√3

  =  700(1 + √3) ==>  700 (1 + 1.732)  =  700 (2.732)

  =  1912.4 m

Width of the river is 1912.4 m.

Problem 3 :

A person X standing on a horizontal plane, observes a bird flying at a distance of 100 m from him at an angle of  elevation of 30°. Another person Y standing on the roof of a 20 m high building, observes the bird at the same time at an angle of elevation of 45°. If X and Y are on the opposite sides of the bird, then find the distance of the bird from Y.

Solution : 

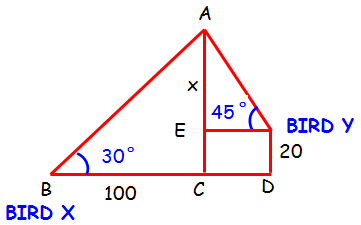
In triangle ABC

∠ABC  =  30°

sin θ = opposite side/Hypotenuse side

sin 30°  =  (AE + EC)/BC

1/2  =  (x + 20)/100

100  =  2 (x + 20)

100  =  2x + 40

100 - 40  =  2x  ==> 2x  =  60  ==> x  =  30

In triangle AYE

∠AYE  =  45°

sin 45°  =  AE /EY

1/√2  =  x / EY

1/√2  =  30 / EY

EY = 30√2

So, the required distance of the bird from Y is 30√2 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.