ANGLE OF ELEVATION AND DEPRESSION QUESTIONS

Question 1 :

The angles of elevation of an artificial earth satellite is measured from two earth stations, situated on the same side of the satellite, are found to be 30° and 60°. The two earth stations and the satellite are in the same vertical plane. If the distance between the earth stations is 4000 km, find the distance between the satellite and earth. (√3 = 1.732)

Solution :

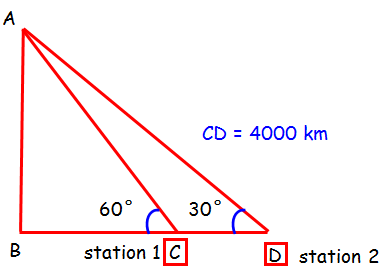
BC = x m

In triangle ABC :

∠ACB  =  60°

  tan θ = opposite side/Adjacent side

tan 60°  =  AB/BC

√3  =  AB/BC

AB = √3BC 

AB = x√3 ----(1)

In triangle ABD :

∠ADB  =  30°

  tan θ = opposite side/Adjacent side

tan 30°  =  AB/BD

1/√3  =  AB/(BC + CD)

1/√3  =  AB/(x + 4000)

AB = (x + 4000)/√3 ---->(2) 

(1) = (2)

 x√3  =  (x + 4000)/√3 

  3 x =  x + 4000

3x - x = 4000

 2x = 4000

x = 2000

distance between the satellite and earth(AB) = x√3

=  2000 (1.732)  =  3464 km

Question 2 :

From the top of a tower of height 60 m, the angles of depression of the top and the bottom of a building are observed to be 30° and 60° respectively. Find the height of the building.

Solution :

From the given information, we can draw a rough diagram 

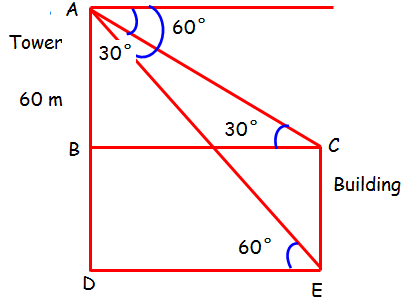
In triangle ABC :

Let AB = x  and BD = 60 - x 

∠ACB  =  30°

  tan θ = opposite side/Adjacent side

tan 30°  =  AB/BC

1/√3  =  x/BC

BC = x √3 ----(1)

In triangle ADE :

∠AED  =  60°

  tan θ = opposite side/Adjacent side

tan 60°  =  AD/DE

√3  =  60/DE

DE = 60/√3 ----(2)

(1)  =  (2)

x √3  =  60/√3

3x = 60

x = 20 m

CE = 60 - 20 = 40 m

Height of the building = 40 m.

Question 3 :

Sarah is standing on a cliff-top and observes the angle of depression to a point A in a deep gorge to be 50°. Sarah then turns in the opposite direction and observes another point B in a second gorge to have an angle of depression of 65°. The points, A and B, are both on the same horizontal level 45m beneath Sarah. Find the distance between A and B.

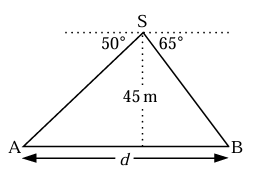
Solution :

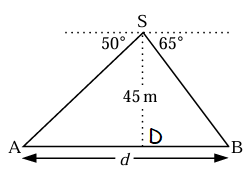
<SAB = 50 and <SBA = 65

Let SD is the height of the triangle with the measure of 45 m.

In triangle SAD :

tan 50 = SD/AD

1.19 = 45/AD

AD = 45/1.19

AD = 37.81

In triangle SDB :

tan 65 = SD/DB

2.14 = 45/DB

DB = 45/2.14

DB = 21.02

AD + DB = AB

AB = 37.81 + 21.02

AB = 58.83

Then distance between A and B is 58.83 m

Question 4 :

At a certain point on a cliff-face, a rock-climber, Rob, observes the base of the cliff opposite to have an angle of depression of 60°. He also observes the top of the same cliff to have an angle of elevation of 40°. He knows that the distance from the base of the cliff he is climbing to the base of the opposite cliff is 110 m.

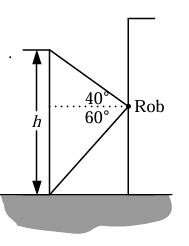
If the cliff that Rob is climbing is 30 m taller than the other, find the height of the smaller cliff.

Solution :

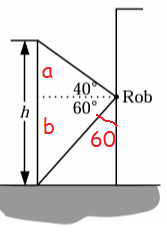
In triangle above, 

tan 40 = opposite side / adjacent side

0.839 = a/110

a = 110(0.839)

a = 92.29

In the triangle below,

tan 60 = b/110

b = 110 tan 60

= 110√3

= 110(1.732)

b = 190.52

a + b = h

h = 92.29 + 190.52

= 282.81

Rob is climbing is 30 m taller than the other,

 = 282.81 + 30

= 312.81 m

Question 5 :

Joy is sitting in a tree-top 3.5 m tall and she observes Fritz the cat on the ground, 2 m from the base of the tree. Calculate the angle of depression from Joy to Fritz.

Solution :

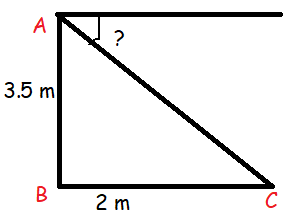
From the above triangle,

 tan C = AB/BC

tan C = 3.5/2

tan C = 1.75

C = tan^-1(1.75)

C = 60.25

So, the required angle of depression is 60.25

Question 6 :

A sailor sights a fortress on top of a 45 m cliff from his position 1.6 km out from the base of the cliff. What is the angle of elevation from the sailor to the fortress?

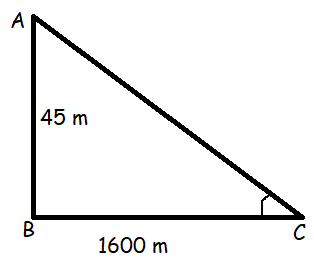
Solution :

tan C = Opposite side / Adjacent side

tan C = 45/1600

tan C = 0.028125

C = tan^-1(0.028125)

C = 1.61 degree.

Question 7 :

Ann is on top of a building and observes a Inman on top of a taller building nearby at an angle of elevation of 16°. If her building is 52m high and the other is 91 m tall, how far in a direct line is Ann from the man?

Solution :

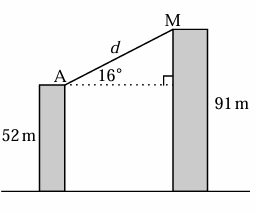
In the triangle above, 

Opposite side = 91 m - 52 m

= 39 m

tan 16 = opposite side  adjacent side

0.286 = 39/adjacent side 

adjacent side = 39/0.286

= 136.36

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.