EXAMPLE PROBLEMS OF ANGLE OF ELEVATION AND DEPRESSION

Example 1 :

A boy standing on the ground, spots a balloon moving with the wind in a horizontal line at a constant height . The angle of elevation of the balloon from the boy at an instant is 60°. After 2 minutes, from the same point of observation, the angle of elevation reduces to 30°. If the speed of wind is 29√3 m/min. then, find the height of the balloon from the ground level.

Solution :

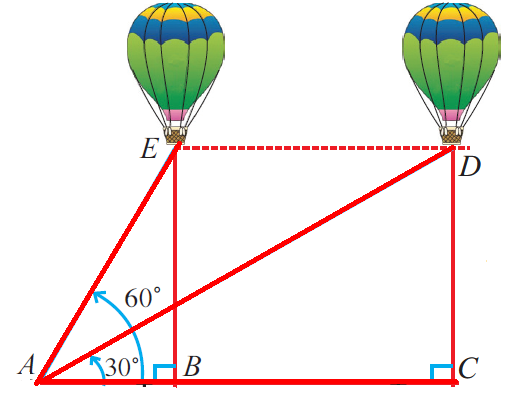
Distance covered by the balloon  =  BC

BC = Time x Speed ==> 2 x 29 √3 ==> 58√3 m

AB = x  then AC = x + 58√3

In triangle DAC :

∠DAC  =  30°

  tan θ = opposite side/Adjacent side

tan 30°  =  DC/AC

1/√3  =  DC/(x + 58√3)

DC = (x + 58√3)/√3 ----(1)

In triangle EAB :

∠EAB  =  60°

  tan θ = opposite side/Adjacent side

tan 60°  =  EB/AB

√3  =  EB/x

x√3  =  EB

 EB  =  √3x ---->(2) 

Since EB = DC

(1) = (2)

(x + 58√3)/√3  =  √3x

 x + 58√3  =  3x

3x - x  =  58√3

2x  =  58√3

x  =   58√3/2 ==> 29√3 m

Height of the balloon from ground level EB  =  √3 x

=  29 √3 (√3)

=  29(3) ==> 87 m

Hence height of the balloon from ground level = 87 m.

Example 2 :

A straight highway leads to the foot of a tower . A man standing on the top of the tower spots a van at an angle of depression of 30°. The van is approaching the tower with a uniform speed. After 6 minutes, the angle of depression of the van is found to be 60°. How many more minutes will it take for the van to reach the tower?

Solution :

From the given information, we can draw a rough diagram 

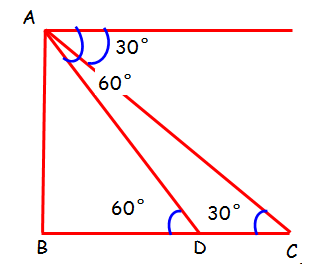
Distance covered by the van to reach D from C = 6 minutes

time taken = x 

Distance between D and C = 6x

In triangle ACB

∠ACB  =  30°

  tan θ = opposite side/Adjacent side

  tan 30° = AB/BC

  1/√3  =  AB/(BD+DC)

1/√3  =  AB/(BD+6x) 

(BD+6x)/√3 = AB ----(1)

In triangle ABD

∠ABD  =  60°

  tan θ = opposite side/Adjacent side

  tan 60° = AB/BD

  √3  =  AB/BD ==> AB  = BD√3  -----(2)

(1) = (2)

(BD+6x)/√3  =  BD√3

BD + 6x = BD(3) 

3BD - BD = 6x

2BD = 6x

BD = 6x /2 = 3x

Here 3 represents number of minutes covered by the van and x stands for time taken.

Hence 3 more minutes will it take for the van to reach the tower.

Example 3 :

A man flies a kite with a 100 foot string. The angle of elevation of the string is 52 degree. How high off the ground is the kite ?

Solution :

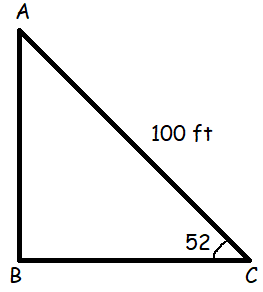
AB = Opposite side

BC = Adjacent side

AC = Hypotenuse

sin θ = opposite side/Hypotenuse

sin 52 = AB/AC

0.788 = AB/100

AB = 0.788(100)

= 78.8 ft

So, height of the kite is at 78.8 ft.

Example 4 :

From a plane flying due east at 265 m above sea level, the angles of depression of two ships sailing due east measure 35° and 25°. How far apart are the ships ?

Solution :

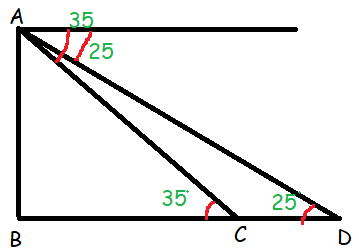
AB = 265 m = Opposite side

BC and BD are adjacent sides

AC and AD are hypotenuse

In triangle ABC,

tan θ = opposite side/adjacent side

tan 35 = AB/BC

tan 35 = 265 / BC

BC = 265/tan 35

BC = 265/0.700

BC = 378.57

In triangle ABD,

tan θ = opposite side/adjacent side

tan 25 = AB/BD

tan 25 = 265 / (BC + CD)

BC + CD = 265/tan 25

378.57 + CD = 265/0.466

378.57 + CD = 568.66

CD = 568.66 - 378.57

CD = 190.09

So, the ships are at 190.09 ft apart.

Example 5 :

From the top of a vertical cliff 40 m high, the angle of depression of an object that is level with the base of the cliff is 34 degree. How far is the object from the base of the cliff ?

Solution :

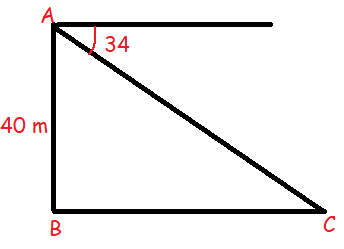
Using parallel lines and transversal, <ACB = 34

AB = Opposite side

BC = Adjacent side 

AC = Hypotenuse

tan 34 = AB/BC

tan 34 = 40/BC

BC = 40/tan 34

BC = 40/0.674

BC = 59.34

So, the distance  between the base of the cliff is 59.34 ft approximately.

Example 6 :

A TV tower stands vertically on a bank of a canal. The tower is watched from a point on the other bank directly opposite to it. The angle of elevation of the top of the tower is 58°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal. (tan 58° = 1.6003)

Solution :

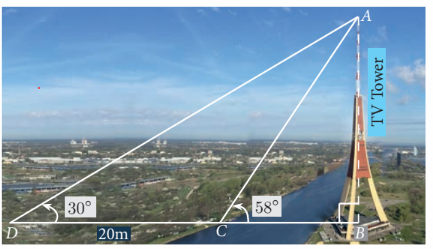
In triangle ABC,

tan 58 = AB/BC

1.600 = AB/BC

AB = BC (1.6) --------(1)

In triangle ADB,

tan 30 = AB/BD

0.577 = AB/(BC + CD)

AB = 0.577(BC + CD)

AB = 0.577(BC + 20) --------(2)

(1) = (2)

Width of the canal :

BC (1.6) = 0.577(BC + 20)

(1.6 - 0.577) BC = 20(0.577)

1.023 BC = 11.54

BC = 11.54/1.023

BC = 11.28

So, width of the canal is 11.28 m

Height of the tower :

AB = BC (1.6)

AB = 11.28(1.6)

AB = 18.04 m

So, height of the tower is 18.04 m

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.