MENSURATION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Mensuration is one of the branches of mathematics.This means measurement.It is is being done in our life in many situations.
For example,
A Length of cloth we need for stitching,the area of a wall which is being painted, perimeter of the circular garden to be fenced, quantity of water needed to fill the tank. For these kind of activities, we are doing measurements for further needs.
Here, we are going to cover three areas here.
1.Perimeter
2.Area
3.Volume
Apart from the examples and practice questions in the above three areas, we also give calculators in this topic which can be used by the students to check their answers which they have found for the questions they have.You can use any of the given calculators to get answer for your questions in seconds.

For example, in his development of integration and calculus, he tried to find a value for π by using circumscribed and inscribed polygons, eventually using 96 sided polygons inside and outside a circle to generate a value for Pi of between 31⁄7 (approximately 3.1429) and 310⁄71 (approximately 3.1408). This range of values is extremely accurate, as the actual value is 3.1416. This is just one example of his inventions.
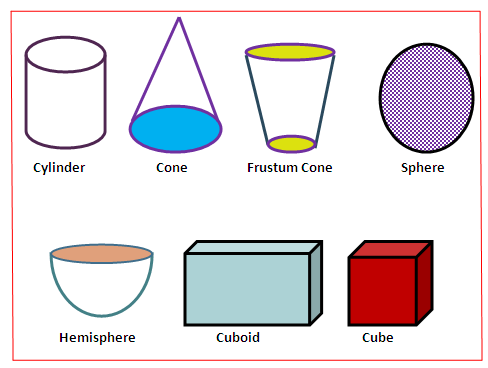
In this topic we are going study about perimeter, area and volume of different shapes like a cylinder, cone, sphere, hemisphere etc..These shapes are called geometric shapes.
Circle
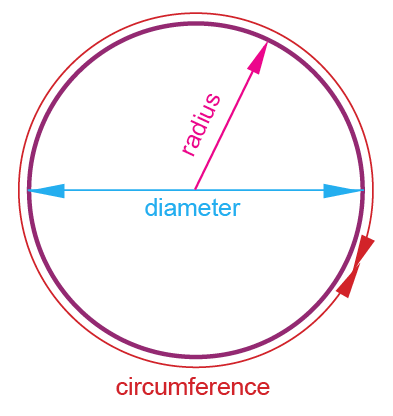
Area of circle = πr2
Circumference of circle = 2πr
Example problems of area of circle
Example problems of circumference of circle
Semi Circle
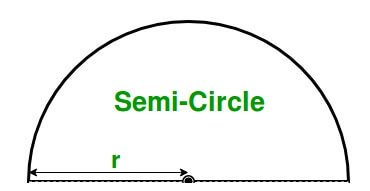
Area of semicircle = πr2/2
Circumference of circle = πr
Example problems on semi circle
Quadrant
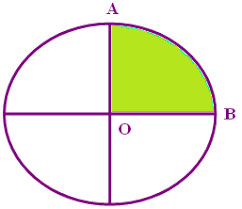
Area of quadrant = πr2/4
Equilateral Triangle
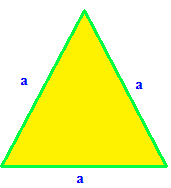
Area of equilateral triangle = (√3/4)a2
Perimeter of equilateral triangle = 3a
Example problems on equilateral triangle
Scalene Triangle
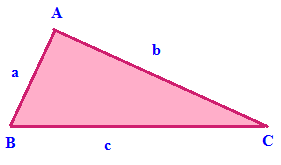
Area of scalene triangle = √[s(s - a)(s - b)(s - c)]
Perimeter of scalene triangle = a + b + c
Example problems on scalene triangle
Right Triangle
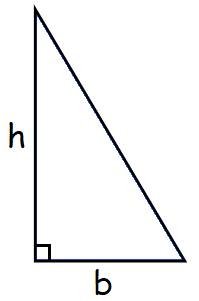
Area of right triangle = (b x h)/2
Parallelogram
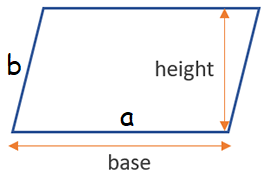
Area of parallelogram = b x h
Perimeter of parallelogram = 2(a + b)
Example problems of perimeter of parallelogram
Quadrilateral
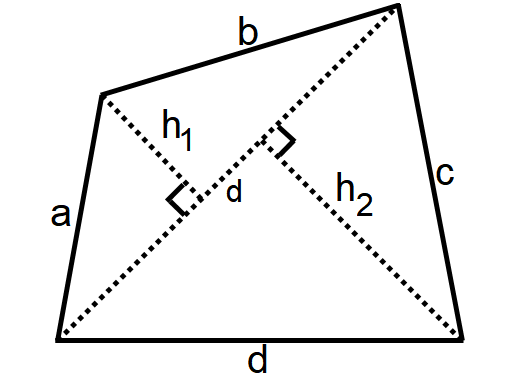
Area of quadrilateral = (1/2) x d x (h1 + h2)
Perimeter of quadrilateral = a + b + c + d
Rectangle
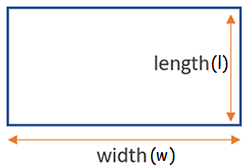
Area of rectangle = l x w
Perimeter of rectangle = 2(l + w)
Examples of perimeter of rectangle
Square
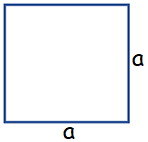
Area of square = a x a
Perimeter of square = 4a
Examples problems on area of square
Examples problems on perimeter of square
Rhombus
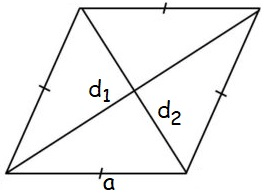
Area of rhombus = (d1 x d2)/2
Perimeter of rhombus = 4a
Examples problems on area of rhombus
Examples problems on perimeter of rhombus
Trapezoid
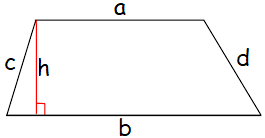
Area of trapezoid = h(a + b)/2
Perimeter of trapezoid = a + b + c + d
Examples problems on area of trapezoid
Sector
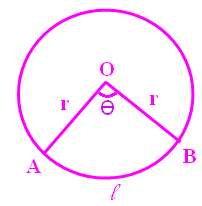
Length of arc (l) = (θ/360) ⋅ 2πr
When we know the radius "r" of the circle and central angle "θ" of the sector :
Area of the sector = (θ/360°) ⋅ πr2
When we know the radius "r" of the circle and arc length "l":
Area of the sector = (l ⋅ r)/2
Worksheet for length of arc
Cylinder
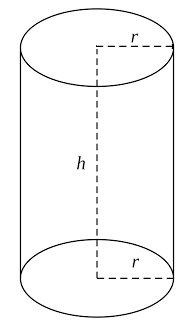
Curved surface area of cylinder = 2πrh
Total surface area of cylinder = 2πr(h + r)
Volume of cylinder = πr2h
Cone
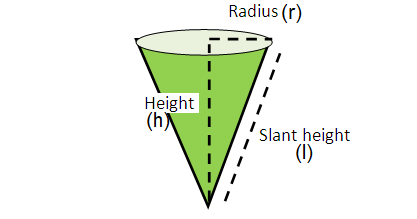
Curved surface area of cone = πrl
Total surface area of cone = 2πr(l + r)
Volume of cone = πr2h/3
Sphere
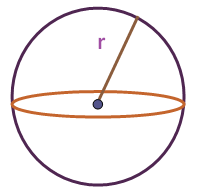
Surface area of sphere = 4πr2
Volume of sphere = 4πr3/3
Hemisphere
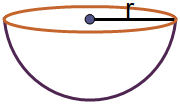
Curved surface area of hemisphere = 2πr2
Total surface area of hemisphere = 3πr2
Volume of hemisphere = 2πr3/3
Mensuration Calculators
18. Heron's Triangle Area Calculator
20. Regular Polygon Area Calculator
22. Circle Sector Area Calculator
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 50)
Mar 06, 26 07:48 PM
Digital SAT Math Problems and Solutions (Part - 50) -
Digital SAT Math Problems and Solutions (Part - 49)
Mar 06, 26 06:47 PM
Digital SAT Math Problems and Solutions (Part - 49) -
Digital SAT Math Problems and Solutions (Part - 48)
Mar 06, 26 05:24 PM
Digital SAT Math Problems and Solutions (Part - 48)


