VENN DIAGRAM OF A DIFFERENCE B

Here we are going to see how to draw a venn diagram of A difference B.

Venn diagram of A difference B :

A\B (or) A - B

To draw a venn diagram for A\B, shade the region of A by excluding the common region of A and B.

A\B (or) A - B

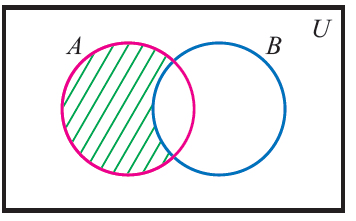
Let A and B be two sets.

Now, we can define the following new set.

A \ B  =  {z | z ∈ A but z ∉ B}

(That is z must be in  A and must not be in B)

A \ B is read as "A difference B"

Now that A \ B contains only elements of A which are not in B and the figure given above illustrates this.

Venn diagram of B\A (or) B - A :

To draw a venn diagram for B\A, shade the region of B by excluding the common region of B and A.

B\A (or) B - A

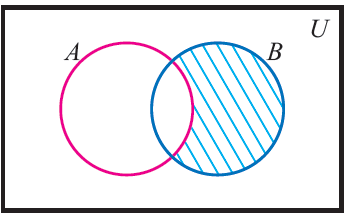
Let A and B be two sets.

Now, we can define the following new set.

B \ A  =  {z | z ∈ B but z ∉ A}

(That is z must be in  B and must not be in A)

B \ A is read as "B difference A"

Now that B \ A contains only elements of B which are not in A and the figure given above illustrates this.

Let us look into some examples to understand the above concepts.

Example 1 :

If A = {- 2, - 1,0,3,4}, B = {- 1,3,5}, find (i) A - B (ii) B - A

Solution :

A = {- 2, - 1,0,3,4} and B = {- 1,3,5}

A - B = { -2, 0, 4}

B - A = { 5 }

Example 2 :

If A = {2, 3, 5, 7, 11} and B = {5, 7, 9, 11, 13} , find A Δ B.

Solution :

A = {2, 3, 5, 7, 11} and B = {5, 7, 9, 11, 13}

A - B = { 2, 3 }

B - A = { 9, 13 }

A Δ B = (A - B) U (B - A)

    =  { 2, 3, 9, 13 }

Example 3 :

Given that U = {3, 7, 9, 11, 15, 17, 18}, M = {3, 7, 9, 11} and N = {7, 11, 15, 17},

find (i) M - N    (ii) N - M     (iii) N' - M     (iv) M' - N

(v) M n (M - N)    (vi) N U (N - M)     (vii) n(M - N)

Solution :

U = { 3, 7, 9, 11, 15, 17, 18 }

M = { 3, 7, 9, 11 }

N = { 7, 11, 15, 17 }

(i) M - N 

The set M - N would contain the elements of the set M excluding the elements of M n N

M - N = { 3, 9 }

(ii) N - M 

The set N - M would contain the elements of the set M excluding the elements of N n M

N - M = { 15, 17 }

(iii) N' - M

N' = { 3, 9, 18 }

N' - M  =  {18} 

(iv) M' - N

M' = { 15, 17, 18 }

M' - N = { 18 }

(v) M n (M - N)

The set M n (M - N) would contain the set of common elements that we found in both the set M and (M - N)

M = { 3, 7, 9, 11 }  M - N = { 3, 9 }

M n (M - N)  =  { 3, 9}

(vi) N U (N - M)

N = { 7, 11, 15, 17 }    N - M = { 15, 17 }

N U (N - M)  =  {  7, 11, 15, 17 }

(vii) n(M - N)

Number of elements of set M - N is 2.

Hence  n(M - N) =  2

Related topics

• Venn diagram A U B
• Venn diagram A n B
• Venn diagram of A'
• Venn diagram of B'
• Venn diagram of (AUB)'
• Venn diagram of (AnB)'
• Venn diagram of A\B
• Venn diagram of B\A

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.