VENN DIAGRAM FOR B COMPLEMENT

Here we are going to see how to draw a venn diagram for A complement.

To draw a venn diagram for B', we have shade the region that excludes B

B'

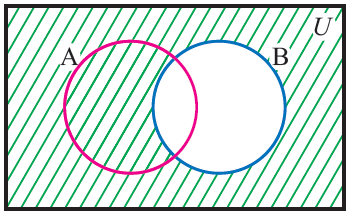
If B ⊆ U, where U is a universal set, then U \ B is called the compliment of B with respect to U. If underlying universal set is fixed, then we denote U \ B by B' and it is called compliment of B.

B'  =  U \ B 

The difference set set B \ A can also be viewed as the compliment of B with respect to A.  

To draw a venn diagram for A', we have shade the region that excludes A

A'

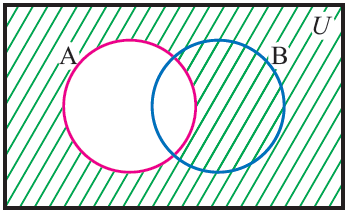
If A ⊆ U, where U is a universal set, then U \ A is called the compliment of A with respect to U. If underlying universal set is fixed, then we denote U \ A by A' and it is called compliment of A.

A'  =  U \ A 

The difference set set A \ B can also be viewed as the compliment of B with respect to A. 

Example 1 :

From the venn diagram, write the elements of the following sets

(i)  A'   (ii)  B'   (iii)  (A n B)'   (iv)  (A U B)'

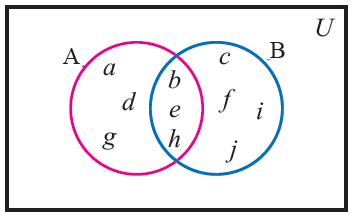
Solution :

(i) A'

A' =  { c, f, i ,j }

(ii)  B'

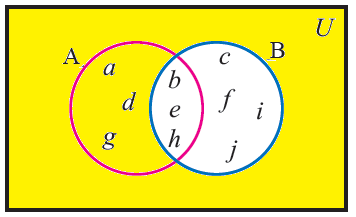
B' =  { a, d, g }

(iii)  (A n B)'

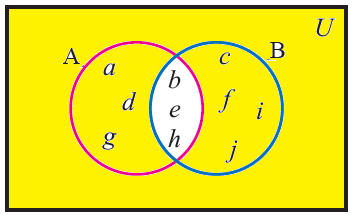
(A n B)'  =  { a, d, g, c, f, i, j }

(iv)  (A U B)'

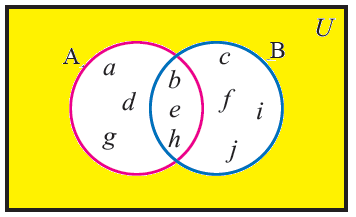
(A U B)'  =  {  }  (or) null set

Example 2 :

If n(U) = 43, n (A) =  26 find n (A')

Solution :

By using the formula,

n (A) + n (A')  =  n (U)

we may find the value of n (A')

26 + n (A') = 43

Subtract 26 on both sides

26 - 26 + n (A')  =  43 - 26

n (A')  =  17

Example 3 :

If n (U) = 38, n (A) = 16, n (A n B) = 12, n (B') = 20, find n (A U B).

Solution :

By using the formula,

n (B) + n (B')  =  n (U)

we may find the value of n (B')

n (B) + 20 = 38

Subtract 20 on both sides

n (B) + 20 - 20  =  38 - 20

n (B)  =  18

n (A U B) = n (A) + n (B) - n (A n B)

= 16 + 18 - 12

=  34 - 12

=  22

Related topics

• Venn diagram A U B
• Venn diagram A n B
• Venn diagram of A'
• Venn diagram of B'
• Venn diagram of (AUB)'
• Venn diagram of (AnB)'
• Venn diagram of A\B
• Venn diagram of B\A

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.