VENN DIAGRAM OF A UNION B WHOLE COMPLEMENT

In this section, you will learn, how to draw a venn diagram for A union B whole complement.

Venn Diagram of (A u B)' : 

To  represent (A u B)' in venn diagram, we have to shade the region other than A and B.

First draw Venn diagram for (A u B) and then (A u B)'. 

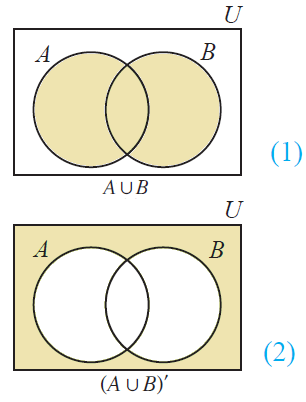
Demorgan's law for (A u B)'.

(A u B)'  =  A' n B'

Lets draw the Venn diagram of (A' n B') and verify the above Demorgan's law. 

We have already drawn venn diagram for (A u B)'. 

Now, let's draw Venn diagram for (A' n  B'). 

Draw Venn diagram for A' and B'.

Then, to draw Venn diagram for (A' n B'), find the common region of A' and B'. 

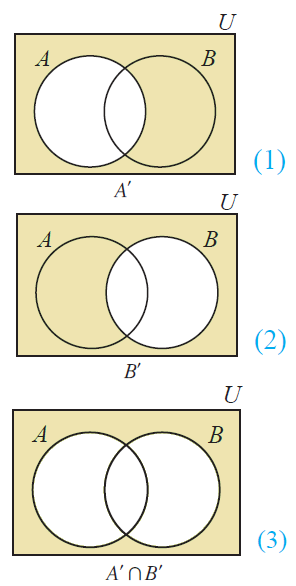
The resulting Venn diagrams of (A u B)' and (A' n B') are same. 

So, 

(A u B)'  =  A' n B'

Practice Problems

Problem 1 :

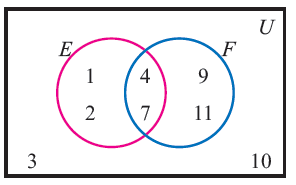
Use the Venn diagram to answer the following questions

(i) List the elements of U, E', F', (E U F)' and (E n F)'

Solution :

(i)  To find the elements of universal set U, we have to list out all the elements that we find in the rectangular box.

U = { 1, 2, 3, 4, 7, 9, 10, 11 }

(ii)  To find the elements of the set E', we have to list out all the elements other than the circle E.

E' = { 3, 9, 10, 11 }

(iii)  To find the elements of the set F', we have to list out all the elements other than the circle F.

F' = { 1, 2, 3, 4, 7, 10 }

(iv)  To find the elements of the set (E U F)', first we have to find the the elements of the set E U F

E U F =  { 1, 2, 3, 4, 7, 9, 10, 11 }

(E U F)' =  {  }

(v)  To find the elements of the set (E n F)', first we have to find the the elements of the set E n F

E n F =  { 4, 7 }

(E n F)' =  { 1, 2, 3, 9, 10, 11 }

Problem 2 :

If U = {x : 1 ≤ x ≤ 10, x ∊ N}, A = {1, 3, 5, 7, 9} and B = {2, 3, 5, 9, 10}, find

(i) A'    (ii) B'     (iii) A' U B'     (iv) A' ⋂ B'

Solution :

U = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }

A = {1, 3, 5, 7, 9}

B = {2, 3, 5, 9, 10}

(i) A' = { 2, 4, 6, 8, 10}

(ii) B' = { 1, 4, 6, 7, 8}

(iii) A' U B' = { 1, 2, 4, 6, 7, 8, 10 }

(iv) A' ⋂ B' = { 4, 6, 8 }

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.